Для нахождения коэффициентов парной и множественной регрессии мы использовали метод наименьших квадратов (МНК). Этот метод приводит к хорошим результатам, если остатки e i удовлетворяют условиям Гаусса–Маркова:
- величины e i являются случайными величинами, распределенными по нормальному закону;
- E e i = 0;
- D e i= s 2 — дисперсия каждого отклонения e i одинакова для всех значений переменной. Это свойство называют гомоскедастичностью или равноточностью;
- cov(e i, e j) = 0 (i ¹ j), так что (при нормальном распределении e i) остатки являются независимыми случайными величинами.
Если D e i= s i 2 и s i различны, то говорят о гетероскедастичности регрессионной модели. В этом случае МНК надо скорректировать. Удобнее всего провести такую коррекцию, используя принцип максимального правдоподобия. Поясним сначала суть этого принципа на простом примере.
Пусть эмпирические данные наблюдений { x1, x2, …, xn } характеризуют случайную величину xÎN (m, s2), для которой математическое ожидание m =Ex и дисперсия s 2=Dx неизвестны и их требуется оценить. Выпишем плотность нормального распределения
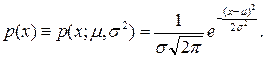
Согласно принципу максимального правдоподобия предполагаем, что функция правдоподобия L=p (x 1) p (x 2) …p (xn) принимает наибольшее значение при истинных значениях параметров m и s2. Удобнее иметь дело с логарифмом этой функции
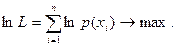
В нашем примере
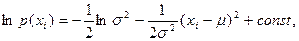
поэтому
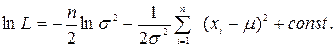
Выпишем необходимые условия экстремума функции ln L (,а значит и L):
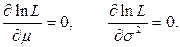
Решение этой системы уравнений после простых преобразований приводит к оценкам
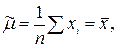
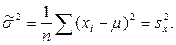
Заметим, что
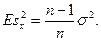
Рассматриваемый пример показывает, что принцип максимального правдоподобия не обязательно приводит к несмещенной оценке искомых параметров.
Воспользуемся принципом максимального правдоподобия для анализа гетероскедастичности. В этом случае модель парной линейной регрессии имеет вид yi=a+bxi+ e i, где E e i= 0, D e i= s i2, так что e i Î N (0, s i2). Соответствующие плотности вероятностей
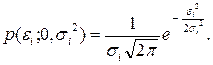
Логарифмическая функция правдоподобия
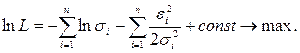
Теперь ясно, как корректируется МНК в случае гетероскедастичности ошибки e i:
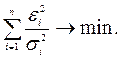
В случае гомоскедастичности дисперсии s i равны и мы получаем классическую формулировку МНК.
Часто вводится веса наблюдений Wi= ls i-2, при этом число l выбирается так, чтобы веса были целыми числами. МНК сводится к минимизации взвешенных сумм квадратов:
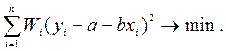
 2014-02-01
2014-02-01 789
789








