Оценка качества уравнения регрессии

После того как найдено уравнение регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

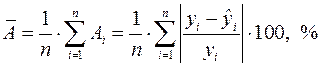. (2.12)

где 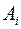 - индивидуальная ошибка аппроксимации.

Если 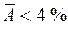 - модель отличного качества; если  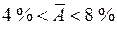- модель хорошего качества; если  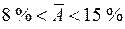- удовлетворительная модель; если 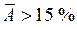- необходимо строить другую модель.

Оценка значимости уравнения регрессии в целом производится на основе 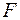- критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной 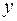 от среднего значения  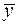раскладывается на две части – «объясненную» и «необъясненную»:

,

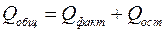где 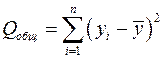 – общая сумма квадратов отклонений;

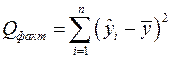 – факторная сумма квадратов отклонений (сумма квадратов отклонений, объясненная регрессией);

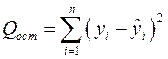 – остаточная сумма квадратов отклонений.

Любая сумма квадратов отклонений связана с числом степеней свободы df, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Разделив каждую сумму квадратов на соответствующее число степеней свободы, получим дисперсию на одну степень свободы.

Схема дисперсионного анализа имеет вид, представленный в таблице 2.1 (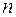 – число наблюдений,  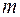– число параметров при переменной ).

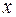Таблица 2.1

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая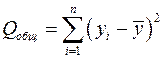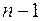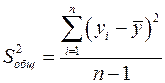
Факторная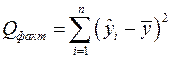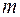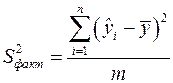
Остаточная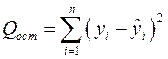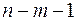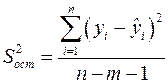

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину 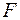- критерия Фишера:

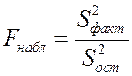. (2.13)

Оценивание качества модели по F -критерию Фишера состоит в проверке гипотезы H₀ о статистической незначимости уравнения регрессии. Для этого наблюдаемое значение 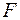-критерия Фишера (2.13) сравнивается с критическим (табличным) значением 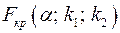при уровне значимости 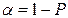и степенях свободы 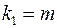и 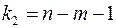. Уровень значимости α – вероятность отвергнуть гипотезу при условии что она верна. Обычно принимается равной 0,05 или 0,01.

Если F_набл > F_кр, то признается статистическая значимость и надежность уравнения регрессии. Если F_набл < F_кр, то признается статистическая незначимость и ненадежность уравнения регрессии.

Величина 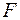- критерия связана с коэффициентом детерминации 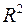, и ее можно рассчитать по следующей формуле:

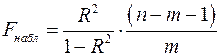. (2.14)

Для парной линейной регрессии 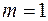, поэтому

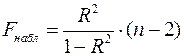. (2.15)

Для оценки статистической значимости параметров уравнения регрессии применяется t -распределение Стьюдента. Величина параметра сравнивается с его стандартной ошибкой, т.е. определяется наблюдаемое (фактическое) значение 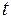- критерия Стьюдента:

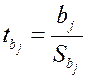, (2.16)

которое затем сравнивается с критическим (табличным) значением 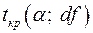 при уровне значимости  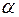и числе степеней свободы .

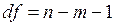Стандартные ошибки параметров линейной регрессии определяются по формулам:

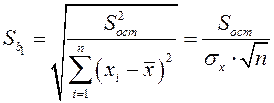, (2.17)

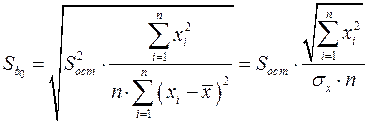. (2.18)

где 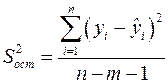– остаточная дисперсия на одну степень свободы. (2.19)

Если | t_набл | > t_кр, то параметр b_j признается статистически значимым. Если | t_набл | < t_кр, то признается статистическая незначимость параметра b_j.

Величина стандартной ошибки совместно с 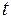-распределением Стьюдента применяется для расчета доверительного интервала параметров регрессии:

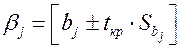. (2.20)

Поскольку знак коэффициента регрессии b₁ указывает на рост результативного признака 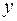 при увеличении факторного признака 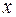(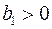), уменьшение результативного признака при увеличении признака-фактора (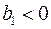) или его независимость от независимой переменной (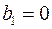) (см. рис. 2.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, 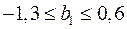. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

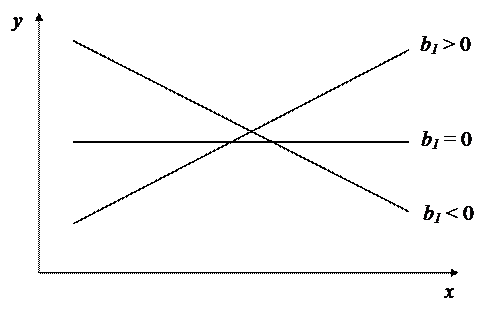Рисунок 2.4 - Наклон линии регрессии в зависимости от значения параметра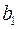

Связь между F -критерием Фишера и t -критерием Стьюдента выражается равенством:

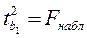. (2.21)

В прогнозных расчетах по уравнению регрессии определяется предсказываемое 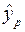значение как точечный прогноз  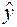при 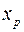, т.е. путем подстановки в уравнение регрессии 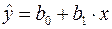соответствующего значения 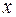. Однако точечный прогноз явно нереален, поэтому он дополняется интервальной оценкой прогнозного значения :

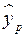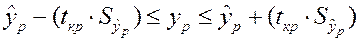, (2.22)

где 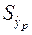– средняя ошибка прогнозируемого индивидуального значения y:

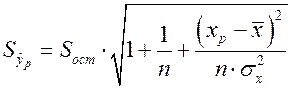. (2.23)