Таблица 4.5
| X | |||||||||||
| Y | 13,3 | 8,9 | 15,1 | 10,4 | 13,1 | 12,4 | 13,2 | 11,8 | 11,5 | 14,2 | 15,4 |
| Z |
Если бы мы построили регрессию Y на X, то получили бы такое уравнение
Y =0,442+0,465 X.
Воспользовавшись моделью с фиктивной переменной получим
Y =0,643+0,466 X -0,422 Z
или для различных стран:
Y K =0,221+0,466 X для Канады и Y A=0,643+0,466 X для Америки.
Экспериментальные данные и три прямые, подобранные методом наименьших квадратов, приведены на рис. 4.3. Все три линии практически параллельны.
Дисперсионный анализ показывает значимость полученных зависимостей, причем уравнение (как с фиктивной переменной, так и без фиктивной переменной) объясняет до 80% вариации относительно среднего.
Вывод, который можно сделать в этом случае - введение фиктивной переменной не дает весомого улучшения модели в смысле дополнительно объясненной вариации.Ñ
Ясно, что для какой-либо задачи существует не единственный способ выбора фиктивных переменных, а в большинстве случаев путей их представления много. Это обстоятельство оказывается выгодным, поскольку в некоторых случаях можно угодить в ловушку, когда существует линейная зависимость между введенными фиктивными переменными.
Чтобы избежать ловушки, необходимо выбрать одну из категорий в качестве эталонной и определять фиктивные переменные для остальных возможных категорий, причем выбор эталонной категории не влияет на сущность регрессии.
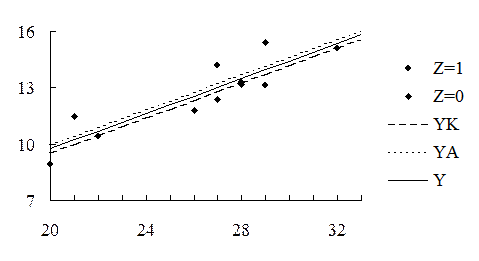
Рис. 4.3
Может потребоваться включение в модель более одной совокупности фиктивных переменных. Это особенно часто встречается при работе с перекрестными выборками. Поясним такую процедуру – множественных совокупностей фиктивных переменных – на примере8.
Пример. Предположим, что исследуется зависимость между весом новорожденного и семейным положением матери, а также рожала ли она раньше.
Введем фиктивную переменную M, которая принимает значения 1, если мать одинока, и 0 – в остальных случаях.
Введем также фиктивную переменную числа родов в прошлом D, равную 1 для матерей, которые рожали в прошлом, и 0 для матерей, которые ранее не рожали.
При этом двойном наборе фиктивных переменных имеется четыре возможных случая с соответствующими комбинациями значений фиктивных переменных:
1. Замужняя мать, первые роды M =0, D =0.
2. Одинокая мать, первые роды M =1, D =0.
3. Замужняя мать, не первые роды M =0, D =1.
4. Одинокая мать, не первые роды M =1, D =1.
Первый случай по смыслу является основной совместной эталонной категорией. Коэффициент при M будет представлять оценку разности веса новорожденных, если мать одинока (ожидаем отрицательный знак коэффициента). Коэффициент при D будет представлять оценку дополнительного веса при рождении, если ребенок не является первенцем. Ребенок для четвертой категории матерей будет подвержен обоим воздействиям. Ñ
Фиктивные переменные могут быть введены не только в правую часть регрессионного соотношения, но и зависимая переменная может быть представлена в такой форме. Это возможно в тех случаях, когда в качестве зависимой переменной мы рассматриваем ответы на вопросы, пользуется ли человек собственной машиной, имеет ли счет в банке и т.п., причем во всех случаях зависимая переменная принимает дискретные значения.
Фиктивные переменные могут быть использованы для учета взаимодействия между различными группами факторов.
Пример. Проиллюстрируем сказанное на примере с окорочками. Для построения двух прямых рассмотрим модель:
Y = b 0+ b 1 X + Z (g 1+ g 2 X)+ u или Y = b 0+ b 1 X + g 1 Z + g 2 XZ + u.
Такой подход позволяет проверить различные варианты гипотез:
1. Гипотеза H0: g 1= g 2=0 против альтернативы H1: что это не так. Если гипотеза H0 будет отвергнута, то мы придем к выводу, что модели не одинаковы, а если нет, то можно пользоваться одной моделью независимо от происхождения окороков.
2. Если гипотеза H0 в предыдущем пункте будет отвергнута, то можно проверить гипотезу H0: g 2=0. Если H0 принимается, то мы заключаем, что имеющиеся два набора данных отличаются только уровнем, имея одинаковые углы наклона.
При необходимости могут быть выбраны и другие варианты проверок, если это разумно для задачи. Получим для указанной выше модели уравнение МНК:
Y =2,974+0,377 X -3,649 Z +0,123(XZ),
причем R 2=0,82.
Два отдельных уравнения для Z =1: Y =-0,675+0,5 X;
и для Z =0: Y =2,974+0,377 X.
Как видно, уравнения несколько отличаются от тех линий, что приведены на рис. 4.3.
Для проверки гипотезы H0: g 1= g 2=0 составим таблицу дисперсионного анализа (табл. 4.6). Значение F =3,399/0,983=3,458, что меньше F 0,05(2; 7)=4,74, а, следовательно, гипотеза H0 принимается, то есть можно пользоваться одной моделью как для окороков из Америки, так и из Канады. Последнее подтверждается ранее полученными результатами.
Как показывает пример, использование взаимодействия с фиктивными переменными упрощает построение подходящих критериев и получение правильных статистик для проверки гипотез. Ñ
 2014-02-01
2014-02-01 732
732








