Тихо Браге (1546 – 1601 гг.)

Тихо Браге родился в семье, принадлежавшей к высшей знати Датского королевства. Он появился на свет в замке Кнудструп, южной части Скандинавского полуострова, которая позже перешла от Дании к Швеции.

В гелиоцентрическую систему Коперника Браге не верил и называл её математической спекуляцией. Хотя к Копернику относился с глубоким уважением, держал в обсерватории его портрет и даже сочинил восторженную оду в его честь.

Тихо Браге, как и Коперник, полагал, что старая планетарная система эпициклов и деферентов слишком сложна и громоздка. И что допущение такого большого количества эпициклов следует считать излишним. Тогда как в предложенной Коперником гелиоцентрической системе оказалось возможным уменьшить общее число кругов (деферентов и эпициклов) до тридцати четырех вместо семидесяти семи кругов геоцентрической теории. Именно своей простотой гелиоцентрическая система Коперника вдохновила Тихо Браге.

В 1588 году, в своем знаменитом труде: «De Mundi aeteri» он предлогает свою компромиссную гео-гелиоцентрическую систему мира, которая представляла собой комбинацию учений Птолемея и Коперника: Солнце, Луна и звёзды вращаются вокруг неподвижной Земли, а все планеты и кометы — вокруг Солнца.

Суточное вращение Земли Браге тоже не признавал.

Подобно системе Коперника такая модель заметно облегчала математические вычисления. И в этом смысле она ничем не отличалась от системы Коперника, однако имела одно важное преимущество, особенно после суда над Галилеем: она не вызывала возражений у инквизиции.

Сам Браге искренне верил в реальность своей системы и перед смертью просил Кеплера поддержать её. Он подробно аргументировал в письмах, почему он считает ошибочной систему Коперника. Один из самых серьёзных аргументов, выдвигаемых Тихо Браге против системы Коперника – это аргумент, связанный с отсутствием годичного параллакса звёзд. С отсутствием годичного кажущегося смещения звезд.

Параллакс (греч. parallaxis уклонение, смещение) — это кажущееся смещение видимого (наблюдаемого) объекта фона в зависимости от нахождения наблюдателя (по причине смещения наблюдателя). Если мы наблюдаем объект под разными углами, с разных точек.

Тихо Браге рассуждал приблизительно так. Если Земля движется относительно Солнца, то вместе с этим движением Земли движемся мы – наблюдатели звезд. А поскольку в ходе движения Земли, мы наблюдаем звезды с разных точек, то нам должно казаться, что эти звезды смещаются. Чего, однако, никогда не происходит. На самом деле нам это не кажется. Звезды всегда остаются на том же самом месте.

Такое рассуждение не выдерживает критики. Оно было бы правильным только в случае относительно небольшого расстояния от Земли до звезд. Определенные Тихо Браге расстояния до звезд, были на несколько порядков меньше действительных. Эти расчеты были осуществлены, исходя из яркости звезд. А точнее сказать, из видимых диаметров звезд. На самом деле видимые диаметры звёзд были увеличены атмосферной рефракцией, которую удалось обнаружить только в XIX веке.

Вообще говоря, для осуществления математических вычислений, которые бы согласовывались с нашими наблюдениями (то есть, другими словами, с точки зрения вычислительной астрономии) – абсолютно не важно, какое из двух тел мы выберем в качестве неподвижной точки отсчета. То есть, совершенно неважно, какое тело, вокруг какого обращается. Но существующий в сознании большинства современных учёных физический взгляд на Вселенную, в соответствии с которым гораздо разумнее считать обращение меньшего по размерам тела (Земли) вокруг большего (Солнца), чем большего вокруг меньшего - заставлял выбрать в качестве неподвижной точки отчета массивное Солнце, а не крошечную Землю.

И еще, одно важное открытие, сделанное Тихо Браге. Он доказал, что никаких твердых небесных сфер – не существует. Тех самых непроницаемых небесных сфер, к которым прикреплены и вместе с которыми движутся все наблюдаемые нами планеты. Пространство между планетами абсолютно пустое.

Во второй половине 16 века над Европой появилась яркая комета. Браге систематически наблюдал за её движением. И в ходе своих наблюдений вдруг понял, что она движется, пересекая небесные сферы. Но как можно пересекать непроницаемые небесные сферы? В случае их наличия они бы оказались непреодолимым препятствием.

Это означало, что Аристотель был не прав: твёрдых небесных сфер не существует, пространство является пустым.

Иоганн Кеплер (1571 – 1630 гг.).

Усовершенствование планетарной системы Коперника было осуществлено только через 70 лет Иоганном Кеплером.

Жизненный путь Кеплера складывался совершенно иначе, чем у Коперника. Последний получил в юности превосходное образование и вел жизнь, полную достатка, что позволяло ему посвящать весь досуг размышлениям над собственной теорией.

Как и Коперник, Кеплер был глубоко верующим человеком. Подобно Копернику, он был убежден, что при сотворении мира Бог следовал какому-то простому и изящному плану, имеющему математический характер. И этот план можно раскрыть с помощью математики. Поскольку наш мир был сотворен в соответствии с неким математическим планом, то в этом мире должна присутствовать математическая гармония. Об этом он и писал в своем первом сочинении «Космографическая тайна» в 1596 году.

В современном понимании этого слова Кеплер настоящим учеными. С одной стороны, он был предельно рационален и одновременно обладал громадной интуицией, что позволяло ему рождать одну за другой новые теоретические схемы. Однако, с другой стороны, понимал, что любая теория должна соответствовать(эмпирическим) наблюдениям. Именно поэтому Кеплер с готовностью жертвовал самыми, казалось бы, многообещающими математическими гипотезами, если видел, что они не согласуются с наблюдательными данными. И с невероятным упорством отказывался мириться с малейшими отклонениями (с мельчайшими несоответствиями с реалиями наблюдаемой нами действительности), которыми любой из современных ученых с легкостью бы пренебрег, если бы речь шла о подтверждении его радикальных идей.

Однако рациональное отношение к миру - пристрастие подгонять свои теории (явления) под заранее уже известные математические схемы, стоило ему нескольких лет безуспешных работ.

Следуя одной из таких схем, Кеплер постулировал, что радиусы орбит шести планет должны совпадать с радиусами сфер, связанных с пятью правильными (Платоновыми) телами. Самый большой радиус имеет сфера Сатурна. В нее вписан куб. В этот куб вписана сфера, радиус которой есть радиус сферы Юпитера. В сферу Юпитера вписан тетраэдр, а в тетраэдр в свою очередь вписана сфера, радиус которой есть радиус сферы Марса, — и так для всех пяти правильных тел. В результате такого построения Кеплер получил шесть сфер — по числу известных тогда планет.

Вскоре Кеплер понял, что его модель при всем своем изяществе не точна. Хотя эта модель воспроизводила движения планет и определяла расстояния между орбитами планет, тем не менее, она воспроизводила движения и определяла расстояния, как говорится, с определенной долей погрешности. Эта определенная доля погрешности, незначительное несоответствие с реалиями наблюдаемой нами действительности – заставило Кеплера отказаться от этой модели.

До этого момента работа Кеплера полностью попадала под критическое замечание Аристотеля относительно пифагорейцев. Аристотель писал: «Пифагорейцы рассматривали явления не ради их самих и не ради того, чтобы докопаться до их причин, а единственно с намерением подогнать явления под свои априорные суждения и попытаться реконструировать мир».

С этого момента Кеплер решил строго следовать наблюдаемым фактам, чтобы с легкостью избавляться от тех теорий, которые не согласуются с нашими эмпирическими наблюдениями. Так или иначе, не соответствуют реалиям наблюдаемой нами действительности.

Такой подход вскоре увенчался успехом. Увенчался открытием трех знаменитых законов движения планет, известных в физике как три закона Кеплера. Первые два закона Кеплер изложил в своем труде «Новая астрономия», опубликованном в 1609 году. Третий закон был изложен Кеплером в его сочинении «Гармония Мира», опубликованном в 1619 году.

Первый закон Кеплера в полном противоречии с традицией вводит в астрономию эллипс. Изучением эллипса занимались еще древние греки примерно за две тысячи лет до описываемых событий, поэтому математические свойства эллипса были хорошо известны.

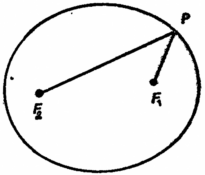
Если окружность можно определить как множество точек, равноудаленных от центра, то эллипс можно определить как множество точек,сумма расстояний от которых (от каждой из которых) до двух заданных точек - постоянна. Таким образом, если F₁ и F₂ — две заданные точки (рис. ниже), а P — произвольная точка эллипса, то сумма PF₁ + PF₂ не зависит от того, где именно расположена точка P на эллипсе.

Две заданные точки F₁ и F₂ называются фокусами эллипса.

Первый закон Кеплера гласит: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Другой фокус — произвольно выбранная точка. Таким образом, после пятнадцати столетий мало успешных попыток воспроизвести движение планет с помощью громоздких комбинаций эпициклов и деферентов на смену этим окружностям пришел простой эллипс.

Первый закон Кеплера говорит нам, по какой орбите (траектории) движется планета, но не говорит о том, с какой скоростью она движется. Можно было бы ожидать, что каждая планета движется по своей орбите с постоянной скоростью, но, как показывали наблюдения — а именно с ними, прежде всего, сверялся Кеплер, — такое предположение не соответствует действительности.

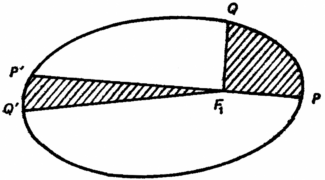
Второй закон Кеплера говорит нам,что если планета перемещается из точки P в точку Q (рис. ниже) за один месяц, а из точки P' в точку Q' также за один месяц, то площади секторов F₁PQ и F₁P^'Q^' должны быть равными.

Из всего сказанного явствует, что планеты движутся по орбитам с переменной скоростью: чем ближе к Солнцу, тем быстрее.

Итак, второй закон Кеплера гласит: если дуги PQ и P'Q' орбиты планета проходит за одно и то же время, то площади секторов F₁PQ и F₁P^'Q^' должны быть равными.

Но одна важная проблема осталась нерешенной. По какому закону устанавливаются (и, таким образом, определяются) расстояния от Солнца до планет? Дело осложнялось тем, что расстояние от планеты до Солнца непостоянно, и Кеплер пытался нащупать новый принцип, который бы отражал это обстоятельство.

Поскольку, по глубокому убеждению Кеплера, наш мир был сотворен в соответствии с неким математическим планом, то в этом мире должна присутствовать математическая гармония. Причем слово «гармония» Кеплер понимал в самом прямом смысле. Подобно Пифагору и пифагорейцам, он верил в существование музыки сфер, которая, хотя и не воспринимаема на слух, но, тем не менее, ее можно обнаружить при надлежащем «переводе» особенностей движения планет на ноты.

Следуя этой идее, Кеплер путем сочетания аргументов математического и музыкального характера пришел ктретьему закону движения планет. Третий закон Кеплера гласит: если T — период обращения планеты вокруг Солнца, a D — ее среднее расстояние от Солнца, то

T² = kD³,

где k — постоянная, одинаковая для всех планет. (В действительности вместо среднего расстояния D следует брать большую полуось эллиптической орбиты планеты.) Такова формулировка третьего закона Кеплера, об открытии которого он торжественно возвестил в своем сочинении «Гармония Мира» в 1619 году.

Среднее расстояние Земли от Солнца равно примерно 150 млн. километров. А период ее обращения вокруг Солнца равен одному году. Подставляя значения D и T для Земли, мы можем вычислить постоянную k. Это означает, что с помощью третьего закона Кеплера мы можем вычислять среднее расстояние от планеты до Солнца, если известен ее период обращения, или, наоборот, период, если известно среднее расстояние.

Галилео Галилей (1564-1642). Родился во Флоренции, в возрасте семнадцати лет поступил в Пизанский университет, намереваясь изучать медицину. В 1609 году в Голландии был изобретен телескоп, и Галилей, прослышав об этом изобретении, сам построил телескоп и приступил к наблюдениям неба. Результаты наблюдений повергли в изумление Галилея. Он обнаружил у Юпитера четыре луны (в современные телескопы мы можем наблюдать 12 спутников Юпитера). Наличие спутника у Земли и наличие спутников у Юпитера означало, что у любой планеты (солнечной системы) могут быть естественные спутники.

Галилей наблюдал неровности и горы на поверхности Луны, пятна на Солнце. Млечный Путь, ранее казавшийся широкой светлой полосой, при наблюдении в телескоп «распался» на мириады звезд.

С помощью телескопа Галилей наблюдал фазы Венеры. Подобно тому, как мы наблюдаем фазы Луны невооруженным глазом. Это подтверждало высказывание Коперника, что если бы человеческое зрение было более острым, то человек мог бы наблюдать фазы Венеры и Меркурия.

Произведенные наблюдения убедили Галилея в том, что гелиоцентрическая система Коперника отражает реальное положение вещей. То есть, полностью соответствует реалиям окружающей нас действительности. В 1632 году он издает главный труд своей жизни «Диалог о двух главнейших системах мира» (понятно, что речь в нем идет о птолемеевой и коперниковой планетарной системе), где он последовательно излагает обе системы. А в конечном итоге решительно выступает в защиту гелиоцентрической, коперниковой, планетарной системы.

Церковь легко соглашалась с тем, что новая система мира проще старой. Она легко ее признавала, но не в качестве системы, которая отражает реальное положение вещей. А в качестве некоего удобного инструмента, позволяющего осуществлять относительно несложные математические вычисления, согласующиеся с нашими наблюдениями. Почему относительно несложные? Они действительно были несложными относительно тех самых громоздких математических вычислений, которые осуществлялись в рамках геоцентрической системы с ее эпициклами и дифферентами.

И то, что церковь легко ее признавала, свидетельствует тот факт, что реформа календаря папой Григорием XIII опиралась на практическое использование именно гелиоцентрической планетарной системы.

К середине XVII века научный мир принял гелиоцентрическую систему. Но опять же, исключительно только по причине ее простоты. Теория Коперника завоевала признание у географов и мореплавателей и опять же исключительно потому, что позволяла им значительно упростить вычисления.

Никто особо не возражал против гелиоцентрической системы Коперника-Галилея, пока Галилей рассматривал ее в качестве удобного математического трюка, «выдуманного для сокращения и удобства вычислений» и имеющего только инструментальное значение. Не возражал до тех самых пор, пока Галилей не стал рассматривать ее в качестве системы, отражающей реальное положение вещей.

Другими словами, не было никаких возражений, пока Галилей действовал в соответствии с линией Осиандера. Протестантского священника, который в своем предисловии к книге Коперника «Об обращении небесных сфер» писал: «гипотезы, содержащиеся в этой работе, не обязательно должны быть истинными, от них требуется лишь одно — давать вычисления, согласующиеся с наблюдениями».

Конечно, сам Галилей был готов подчеркивать превосходство системы Коперника в качестве инструмента для вычислений. Но в то же время он верил в то, что она отражает реальное положение вещей. Дает истинное описание мира. А это для него это было гораздо важнее.

И у него действительно были существенные основания верить в истинность этой теории. В качестве этаких оснований выступали его астрономические наблюдения.

Поскольку в наши дни мы воспринимаем гелиоцентрическую теорию и законы Кеплера как нечто бесспорное, нам трудно по достоинству оценить значение достижений Коперника, Галилея и Кеплера. Поэтому всегда следует рассматривать ту обстановку, в которой работали эти великие преобразователи астрономии.

Геоцентрическая планетарная система, господствующая со времен Птолемея и являющаяся частью в системе представлений об окружающем нас мире того времени, утверждала, что Земля находится в центре мироздания и род человеческий — главное действующее лицо в мире. Именно для нас, людей, были сотворены Солнце, Луна и звезды. Гелиоцентрическая теория, отвергая эту основополагающую догму, низводила человечество до жалкой роли малозначащего пятнышка пыли на одном из многих шаров, вращающихся в бескрайних просторах Вселенной.

Какие основные аргументы того времени выдвигались против гелиоцентрической системы? Надо отдать им должное, но выдвигались весьма разумные возражения, имеющие научный характер.

Выдвигался, к примеру, аргумент, который впоследствии использовал Тихо Браге. Это аргумент, который был связан с отсутствием годичного параллакса, то есть, кажущегося смещения звезд. Как уже было указано выше, параллакс – это кажущееся смещение наблюдаемого объекта по причине смещения самого наблюдателя.

Сторонники этого аргумента рассуждали приблизительно так. Если Земля движется относительно Солнца, то вместе с этим движением Земли движемся мы – наблюдатели звезд. А поскольку в ходе движения Земли, мы наблюдаем звезды с разных точек, то нам должно казаться, что эти звезды смещаются. Чего, однако, никогда не происходит. На самом деле нам это не кажется. И, следовательно, Земля неподвижна.

Такое рассуждение было бы правильным только в случае относительно небольшого расстояния от Земли до звезд. О чем и говорил Коперник в ответ на этот аргумент, ссылался на то, что расстояния до звезд огромны по сравнению с размерами орбиты Земли. Объяснение, предложенное Коперником, оказалось правильным. Хотя он был бы очень изумлен, доведись ему узнать, что предполагаемые им расстояния до звезд были на несколько порядков меньше действительных.

Весьма неприятен был и другой аргумент, сводящийся по сути своей к вопросу о том: почему предметы не срываются с движущейся по орбите Земли и не улетают в космическое пространство? Этот вопрос был неслучайным. Он был связан с существовавшим на тот момент предположением, что скорость любого тела пропорционально его массе. Сторонники этого аргумента рассуждали приблизительно так. Если бы Земля двигалась, то она оставила бы далеко позади более мелкие и, соответственно, легкие тела и, соответственно, обладающие меньшей скоростью тела в виде людей и животных, некогда находящиеся на ее поверхности.

Далее следовал другой аргумент - почему Земля не разлетается на части во время своего вращения? В ответ на последний вопрос Коперник заметил, что вращение как естественное движение не может приводить к разрушению тела, и в свою очередь выдвинул контраргумент, задав каверзный вопрос: почему небо не разлетается на части от очень быстрого суточного вращения, которое предполагает геоцентрическая теория?

Остались без ответа следующие аргументы, выдвигаемые против гелиоцентрической системы:

1. Если Земля вращается с запада на восток, то подброшенный в воздух предмет должен был бы упасть к западу от места броска.

2. Почему никто не ощущает ни суточного вращения Земли, ни ее обращения вокруг Солнца? В то же время все «собственными глазами» могут наблюдать движение Солнца.

3. Каким образом была приведена в движение и поддерживается в таком состоянии тяжелая материя Земли?

Тем не менее, на все эти возражения у Коперника и Кеплера был один неотразимый ответ. Каждому из них удалось достичь математического упрощения. Создать систему, которая позволяла делать достаточно простые математические вычисления, которые согласовывались с нашими эмпирическими наблюдениями. Достаточно простые по сравнению с теми математическими вычислениями, которые осуществлялись в рамках геоцентрической системы с ее эпициклами и дифферентами.

Коль скоро поиск математического плана, по которому Бог сотворил мир — цель всякой научной работы. Коль скоро новое математическое описание гораздо проще и потому совершеннее прежних. То уже одно это должно было перевесить в глазах Коперника и Кеплера любые возражения.