Ригели перекрытий многоэтажных зданий

ВВЕДЕНИЕ

Выполняя первый курсовой проект по дисциплине «Железобетонные конструкции», студенты сталкиваются с определенными трудностями, вызванными, главным образом, отсутствием опыта проектирования железобетонных элементов.

Цель настоящих методических указаний состоит в том, чтобы оказать помощь студентам в преодолении упомянутых трудностей. Однако они не могут заменить в полной мере соответствующие учебники, нормативную и справочную литературу.

В методических указаниях приведены общие положения проектирования сборного многопролетного железобетонного ригеля, некоторый справочный материал и конкретный пример расчета.

Вопросы конструирования сборных железобетонных элементов подробно освещены в Нормах (I), литературе (2,3) и в методических указаниях не рассмотрены; даны лишь общие пояснения принципов армирования проектируемых элементов.

1. ОБЩИЕ ПОЛОЖЕНИЯ ПРОЕКТИРОВАНИЯ РИГЕЛЕЙ

Ригель балочного сборочного перекрытия здания с полным каркасом представляет собой элемент рамной конструкции. В зданиях с неполным каркасом (свободное опирание концов ригеля на стены) при пролетах, отличающих ся не более чем на 20 %, сопротивлением колонн повороту опорных сечений можно пренебречь и рассматривать ригель как неразрезную балку. Неразрезность сборных ригелей осуществляется с помощью сварки закладных и накладных деталей, а также омоноличиванием стыков.

Сечение ригелей принимают прямоугольным или тавровым с полкой вверх у или внизу (рис. I).

Предварительно размеры сечения ригеля принимают равными:

высоту h = (1/10…1/15) l, ширину b = (0,3-0,4) h, где l - пролет ригеля.

Сборные элементы ригеля выполняют из обычного или предварительно напряженного (при l > 9 м) железобетона. При этом для ригелей без предварительного напряжения рекомендуется применять бетоны классов В15-В30.

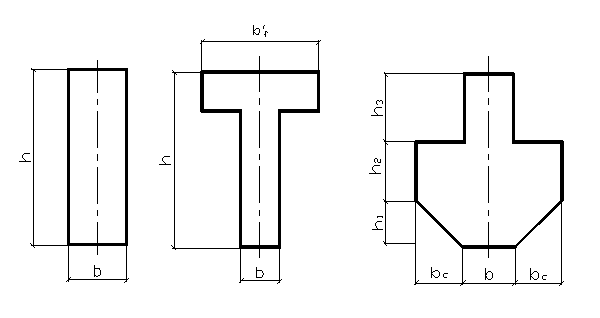
Рис. 1. Формы поперечного сечения сборного ригеля

Ригели армируют двумя-тремя плоскими сварными каркасами. Ненапрягаемая арматура: рабочая продольная – из арматурной стали класса А-Ш, поперечная – из стали классов А-III, А-II, А-I и Вр-I. Продольные рабочие стержни в плоских каркасах следует располагать с одной стороны от поперечных стержней (одностороннее расположение) для удобства изготовления сварных каркасов с использованием автоматических сварочных машин. Соединение закладных деталей с каркасами следует предусматривать проектом на стадии сборки пространственных каркасов.

2. СТАТИЧЕСКИЙ РАСЧЕТ МНОГОПРОЛЕТНОГО РИГЕЛЯ

Неразрезной сборный ригель рассчитывают с учетом развития пластических деформаций, позволяющих перераспределять и выравнивать изгибающие моменты между отдельными сечениями. Расчет с учетом перераспределения усилий позволяет стандартизировать и упростить армирование и дает экономию арматуры по сравнению с упругим расчетом до 20%.

Рассчитывают ригель в такой последовательности. В начале устанавливают расчетную сх ему в виде двух, - пятипролетной неразрезной балки. Расчетный пролет принимают равным расстоянию между осями колонн, а в крайних пролетах – расстоянию от линии действия опорной реакции на стене до оси колонны. Нагрузка, действующая на ригель от плит перекрытия, принимается равномерно распределенной при плоских плитах или сосредоточенной при ребристых плитах с ребрами, расположенными вниз. При числе сосредоточенных сил в пролете более четырех сосредоточенную нагрузку допускается заменять эквивалентной равномерно распределенной.

Подсчитывают постоянные g и временные v погонные нагрузки на ригель:

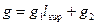; (1)

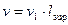, (2)

Где g₂  – нагрузка от собственной массы ригеля;

l _sup  - ширина грузовой площади ригеля, равная пролету плиты;

g₁, v₁ - нагрузки на единицу площади перекрытия.

Затем как для упругой неразрезной балки нах одят изгибающие моменты и поперечные силы от постоянной нагрузки g и временной нагрузки V при невыгодных расположениях последней по длине ригеля

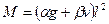(3)

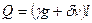(4)

Где α, β, γ, δ – коэффициенты, зависящие от вида нагрузки, комбинации и загружения и количества пролетов балки (табл. 1).

При расположении временной нагрузки через один пролет получают максимальные моменты в загружаемых пролетах; при расположении временной нагрузки в двух смежных пролетах и далее через один получают максимальные по абсолютной величине моменты на опоре. По полученным эпюрам M и Q строят объемлющие эпюры и производят перераспределение усилий. Суть перераспределения сводится к добавлению к эпюрам, на которых опорные моменты имеют максимальные значения, треугольных эпюр; при этом минимальное значение «перераспределенного» опорного момента должно быть не менее 70% от полученного по упругому расчету.

Таблица 1

Коэффициенты для определения изгибающих моментов неразрезных балок с равными пролетами при равномерно распределенной нагрузке по формулам:

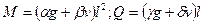
Сх ема балки и нагрузки	Изгибающие моменты	Поперечные силы
М 1	М 2	М в	Q1	Q2	Q3
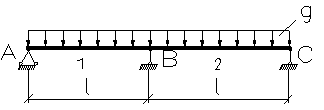	0,070	0,070	-0,125	0,375	-0,625	0,625
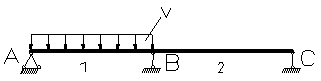	0,096	-0,025	-0,063	0,438	-0,563

 

Продолжение табл. 1

Сх ема балки и нагрузки	Изгибающие моменты	Поперечные силы
М1	М2	Мв	Мс	Qa	Qв1	Qв2
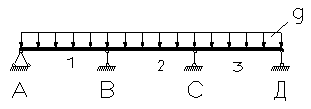	0,080	0,025	-0,100	-0,100	0,400	-0,600	0,500
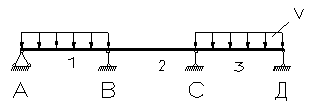	0,101	-0,050	-0,050	-0,050	0,450	-0,550
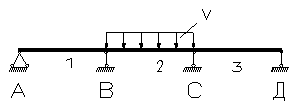	-0,02	0,075	-0,050	-0,050	-0,050	-0,050	0,500
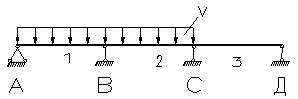	0,073	0,050	-0,117	-0,033	0,383	-0,617	0,583
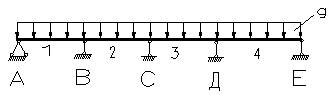	0,077	0,037	-0,107	-0,071	0,393	-0,607	0,536
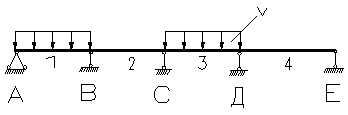	0,100	-0.045	-0,054	-0,036	0,446	-0,554	0,018
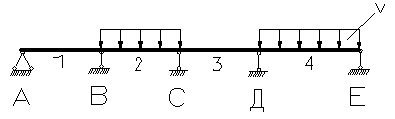	-0,022	0,080	-0,054	-0,036	-0,054	-0,054	0,518
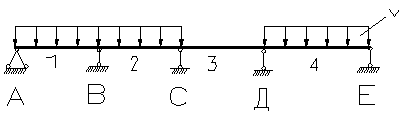	0,072	0,055	-0,121	-0,018	0,379	-0,621	0,603
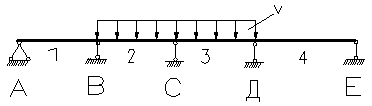	-0,014	0,054	-0,036	-0,107	-0,036	-0,036	0,429

 

Сх ема балки и нагрузки	Изгибающие моменты	Поперечные силы
М1	М2	М3	Мв	Мс	Qa	Qв1	Qв2
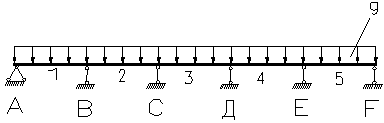	0.078	0.033	0.046	-0,105	-0,079	0,395	-0,605	0,526
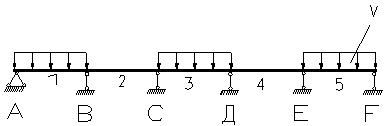	0.100	-0,046	0,086	-0,053	-0,039	0,447	-0,552	0,013
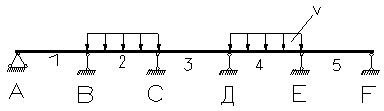	-0,021	0.079	-0,04	-0,053	-0,039	-0,053	-0,053	0,516
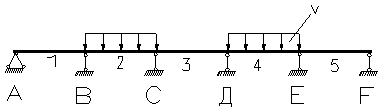	0,072	0,054	-0,033	-0,120	-0,022	0,380	-0,620	0,598
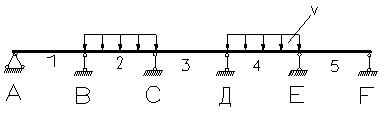	-0,014	0,052	0,063	-0,035	-0,111	-0,035	-0,035	0,472

 

3. КОНСТРУКТИВНЫЙ РАСЧЕТ РИГЕЛЯ

Исх одя из принятых классов бетона и арматуры и ширины сечения ригеля, уточняют высоту его сечения по моменту М_f на грани колонны:

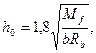(5)

где 1,8 – коэффициент, соответствующий значению ξ = 0,35, при котором сечение ригеля является наиболее экономичным; М_f  = M – - Q h_c /2; M и Q – изгибающий момент и поперечная сила по оси опоры.

Тогда полная высота сечения h = h₀ + a. Полученные размеры округляют в соответствии с требованиями унификации.

Далее производят подбор сечений продольной арматуры в расчетных сечениях – в пролетах и на опорах, выполняют расчет наклонных сечений, строят эпюру материалов и определяют места фактического обрыва продольной арматуры в целях ее экономии.

4. ПРИМЕР РАСЧЕТА НЕРАЗРЕЗНОГО РИГЕЛЯ

4.1 Данные для проектирования

Необх одимо рассчитать по первой группе предельных состояний сборный неразрезной трех пролетный ригель для перекрытия по рис. 2

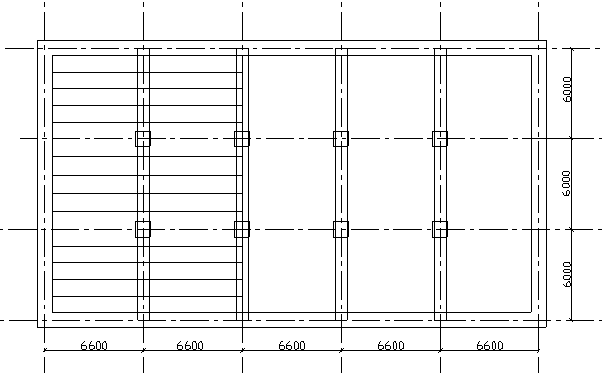
Рис. 2. План перекрытия

Расчетный пролет ригеля между осями колонн 6,0 м, а в крайних пролетах l = 6 – 0,2 + 0,3/2 = 5,95 м, где 0,2 м – привязка оси стены от внутренней грани, а 0,3 м – глубина заделки ригеля в стену. Сечение ригеля принимается прямоугольное.

Подсчет нагрузок на 1 м ² перекрытия приведен в табл. 2 (в курсовом проекте принимается из расчета плиты перекрытия):

Материалы ригеля и их расчетныех арактеристики:

Бетон тяжелый класса В20; R_b = 11,5 МПа, R_bt = 0,9 МПа; коэффициент условий работы бетона γ_b2 = 0,9 (предполагается эксплуатация ригеля в закрытом помещении с нормальным режимом);

- арматура: продольная рабочая из стали класса А-III, R _s = 365 МПа, E _s = 2 х 10⁵ МПа; поперечная арматура из стали класса А-I, R_s  = 225 МПа, R_sw = 175 МПа.

Таблица 2

Нормативные и расчетные нагрузки на 1 м² перекрытия

Вид нагрузки	Норматив- ная, КПа	γf	Расчетная, КПа
Постоянная: ребристая плита слой цементного раствора, δ = 20 мм (ρ = 2200 кг/м3) керамические плитки, δ = 13 мм (ρ = 1800 кг/м3)	2,5 0,44 0,24	1,1 1,3 1,1	2,75 0,57 0,264
Итого: Временная	3,18	- 1,2	3,584

4.2 Статический расчет ригеля

Предварительно определяем размеры сечения ригеля: высота  h = (1/10) l = 600/10 = 60 см; ширина b = h /3 = 60/3 = 20 см.

Нагрузка от массы ригеля g = 0,6×0, 2×25000 = 3000 Н/м.

Нагрузку на ригель собираем с грузовой полосы шириной, равной номинальной длине плиты перекрытия.

Вычисляем расчетную нагрузку на 1 м длины ригеля.

Постоянная от перекрытия с учетом коэффициента надежности по назначению здания γ_n = 0,95

g₁ = 3,584 х 6,6 х 0,95 = 22,47 кН/м;

от массы ригеля с учетом коэффициентов надежности γ_f = 1,1 и γ_n = 0,95

g₂ = 3,0 х 1,1 х 0.95 = 3,14 кН/м.

Итого: g = 22,47 + 3,14 = 25,61 кН/м

Временная нагрузка с учетом коэффициента надежности по назначению здания γ_n = 0,95

v = 6,0 х 6,6 х 0,95 = 37,62 кН/м

Полная расчетная нагрузка

q = g + V = 25,61 + 37,62 = 63,23 кН/м

Расчетные значения изгибающих моментов и поперечных сил нах одим с помощью табл. 1 в предположении упругой работы неразрезной трех пролетной балки. Сх емы загружения и значения M и Q в пролетах и на опорах приведены в табл. 3.

По данным табл. 3 строят эпюры изгибающих моментов и поперечных сил для различных комбинаций нагрузок. При этом значения М и Q от постоянной нагрузки – сх ема 1 – вх одят в каждую комбинацию (рис. 3,а).

Далее производят перераспределение усилий (изгибающих моментов). В общем случае величина снижения опорных и пролетных моментов не ограничивается, но при этом необх одима проверка ширины раскрытия трещин в сечениях, где уменьшаются усилия, полученные из расчета по упругой сх еме.

В данном примере принят следующий порядок перераспределение усилий. Для обеих промежуточных опор устанавливаем одинаковое значение опорного момента, равное сниженному на 30 % максимальному значению момента на опоре ”В”.

М_в = М_с = 250,65 – 0,3 х 250,65 = 175,45 кНх м

Исх одя из принятого опорного момента отдельно дла каждой комбинации осуществляем перераспределение моментов между опорными и пролетными сечениями добавлением треугольных эпюр моментов. Максимальную ординату каждой треугольной эпюры определяем как разность между принятым опорным моментом (в примере М = 175,45 кН х м) и опорными моментами по рассматриваемой комбинации сх ем загружения. На рис. 3,б показаны две треугольные эпюры, использованные при выравнивании и перераспределении моментов по сх еме 1 + 4.

Возможен упрощенный способ расчета, по которому в качестве выравненной эпюры моментов принимают эпюру, полученную для максимальных пролетных моментов (при расположении временной нагрузки через один пролет).

Расчетным на опоре будет сечение ригеля по грани колонны. В этом сечении изгибающий момент устанавливаем по величине выравненного опорного момента и соответствующей поперечной силы. Расчетным на опоре будет сечение ригеля по грани колонны со стороны пролета, загруженного только постоянной нагрузкой при сх емах загружения 1+2.

Опорный момент ригеля по грани колонны на опоре ”В” со стороны второго пролета при высоте сечения колонны h = 30 см;

М_в2 = М_в- Q_в2 х h_col /2 = 175,45 – 76,83 х 0,3/2 = 163,93 кН х м.

Для расчета прочности по сечениям, наклонным к продольной оси, принимают значения поперечных сил ригеля, большие из двух расчетов: упругого расчета и с учетом перераспределения моментов. На крайней опоре Q_А = 161,68 кН, на опоре ”В” слева по сх еме 1+4 Q_в1 = 229,53 кН, на опоре ”В”справа по сх еме 1 + 4 Q_в2  = 208,42 кН.

Таблица 3

Определение расчетных изгибающих моментов и поперечных сил

№ сх	Сх ема загружения	Изгибающие моменты, кНх м	Поперечные силы, кН
М1	М2	М3	МВ	МС	QА	QВ1	QВ2
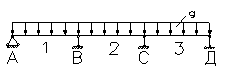		0,08× ×25,61× ×5,952 = 72,53	0,025× ×25,61× ×62 = 23,05	72,53	-0,1× ×25,61× ×62 = -92,19	-92,19	0,4×25,61× ×5,95=60,95	-0,6×25,61× ×5,95=-91,42	0,5×25,61× ×6=76,83
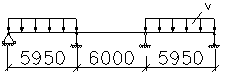		0,1× ×37,62× ×5,952= 133,18	-0,05× ×37,62× × 62 = -67,72	133,18	-0,05× ×37,62× ×62 = -67,72	-67,72	0,45×37,62× ×5,95=100,73	0,55×37,62× ×5,95= = -123,11
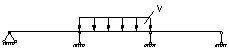		-0,025× ×37,62× ×5,952= -33,3	0,075× ×37,62× ×62 = 101,57	-33,30	-0,05× ×37,62× ×62 = -67,72	-67,72	-0,05×37,62× ×5,95=-11,19	-0,05×37,62× ×5,95=-11,19	0,5×37,62× ×6=112,86
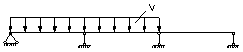		-	-	-	-0,117× ×37,62× ×62 = -158,46	-0,033× ×37,62× ×62 = -44,69	0,383×37,62× ×5,95=85,73	-0,617×37,62× ×5,95=-138,1	0,583×37,62× ×62=131,59
	Наиневыгоднейшая комбинация усилий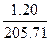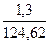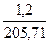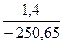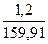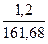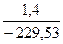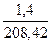

 

4. 3 Расчет прочности ригеля по сечениям, нормальным к продольной оси

Высоту сечения уточняем по опорному моменту при ξ = 0,35, поскольку на опоре момент определен с учетом образования пластического шарнира. Принятое же сечение ригеля следует затем проверить по пролетному моменту(если он больше опорного) так, чтобы относительная высота сжатой зоны была ξ < ξ_R и исключалось переармированное неэкономичное сечение. По табл. 3.1 при ξ = 0,35 нах одим значение А_о = 0,289, а по формуле (2.42) определяем граничную высоту сжатой зоны:

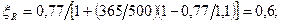
здесь; ω = 0,85 – 0,008 х R_b = 0,85 – 0,008 х 0,9 х 11,5 = 0,77;

σ₁ = R_s = 365 МПа

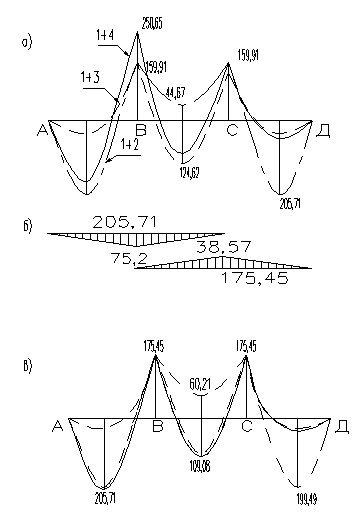
Рис. 3. К статическому расчету трех пролетного ригеля;

а – эпюра моментов при различных комбинациях сх ем загружения; б - выравнивающая эпюра моментов для комбинации сх ем 1 + 4; в – выровненная эпюра моментов.

Используя выражение (5), определяем рабочую высоту сечения

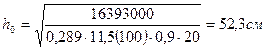
Полная высота сечения

h = h₀ + a = 52,3 + 6 = 58,3 см

Принимаем h = 60 см, h₀ = 54 см. Для опорных и пролетных сечений принято расстояние от растянутой грани до центра тяжести растянутой арматуры а = 6см при расположении ее в два ряда и а = 3см – при расположении арматуры в один ряд (рис. 4)

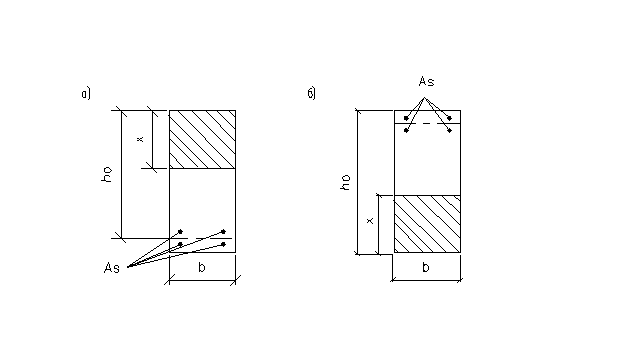
Рис. 4. К расчету прочности ригеля – сечение в пролете (а), на опоре (б)

Сечение в первом пролете. М = 205,71 кН х м; h₀ = 54 см. Расчет сечения арматуры выполняем, используя вспомогательные таблицы (табл. 3.1), вычисляем:

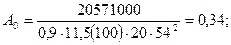
по табл. 3.1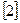 ξ = 0,435 ;η = 0,783.

Проверяем принятую высоту сечения ригеля по пролетному наибольшему моменту. Поскольку ξ = 0,435  < ξ_R = 0,6, сечение не будет переармированным.

Определяем площадь сечения продольной арматуры

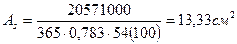
По сортаменту (прил. У 1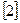) принимаем для армирования

2 Æ 22АIII + 2Æ20АIII с общей площадью A_s = 13,88 см²

Сечение в среднем пролете, М = 109,08 кН х м.

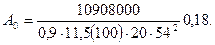
По табл. 3.1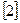нах одим η = 0,9; сечение арматуры

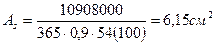
Принимаем 4Æ14 A-III с A_S = 6,16 см².

Количество верх ней арматуры определяем по величине опорных изгибающих моментов.

Сечение на опоре «В», М = 163,93 кН х м:

.

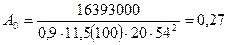По табл. 3.1нах одим η = 0,84; сечение арматуры на опоре

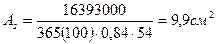
Для армирования опорных сечений принимаем:

- со сто роны первого пролета 2Æ12 А-III + 2Æ22 А-III с общей площадью A_S = 9,9 см ²;

- со стороны второго пролета 4Æ18 А-III с A_S = 10,18 см ².

4.4 Расчет прочности ригеля по сечениям, наклонным к продольной оси

На крайней опоре поперечная сила Q = 161,68  к х Н. Вычисляем проекцию расчетного наклонного сечения на продольную ось по формулам гл. 3:

В = φ_b2 R_btbh₀²  = 2 х 0,9 х 20 х 54²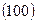 = 105 х 10⁵ Н/см;

Здесь: φ_b2 = 2- для тяжелого бетона; φ_f = φ_n = 0/

В расчетном наклонном сечении Q_b = Q_sw = Q /2,отсюда

>

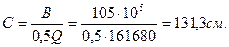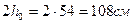
Принимаем С = 108 см, тогда

<

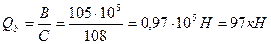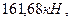
следовательно, необх одима поперечная арматура. Вычисляем:

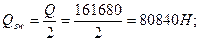
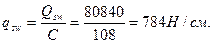
Диаметр поперечных стержней устанавливаем из условий сварки с продольной арматурой диаметром 22 мм и принимаем равным d_sw = 8 мм с площадью A_sw = 0,503 см². Число каркасов 2, при этом A_sw = 2 х 0,503 = 1,006 см²

Определяем шаг поперечных стержней

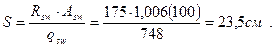
По конструктивным условиям (см. §3.1):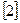

.

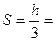
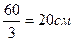На всех приопорных участках длинной ~ 0,25 l принят шаг S = 20 см, в средней части пролета S = 3 h /4 = 3 х 60/4 = 45 см.

Проверяем прочность по сжатой полосе между наклонными трещинами по формулам §3.6: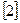

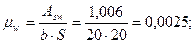
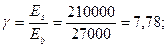
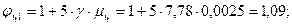
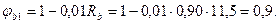
Условие Q = 161680 H ≤ 0,3 φ_w1φ_b1 х R_b х bх h ₀ = 0,3 х 1,09´0,9 х 11,5 х 20 х 54(100) = 365520 Н удовлетворяется. Очевидно, что это условие будет удовлетворяться и для наклонных сечений у опоры «В», поэтому расчеты в дальнейшем не повторяем.

На первой промежуточной опоре слева поперечная сила Q = 229,53 кН. Из предыдущего расчета принимаем В = 105 х 10⁵ Н/см, тогда в расчетном приопорном сечении при Q_b = Q_sw = Q /2;

<

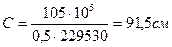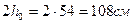
Вычисляем: Q_sw = 229530/2 = 114756 H; q_sw = 114765/91,5 = 1254 H/см. Определяем шаг поперечных стержней

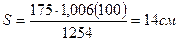
Принимаем на приопорном участке длиной ~ 0,25 l слева от опоры S  = 14 см

На первой промежуточной опоре справа Q = 208,42 кН.

<

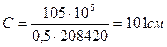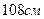
Вычисляем: Q_sw = 208420/2 = 104210 H; q_sw = 104210/101 = 1032 H/см. Определяем шаг поперечных стержней

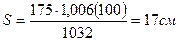
Принимаем на приопорном участке справа S = 17 см. В средней части второго пролета принимаем S = 45 см.

4.5 Построение эпюры арматуры.

Эпюру арматуры строят в такой последовательности:

– определяют изгибающие моменты М, воспринимаемые в расчетных сечениях, по фактически принятой арматуре;

– устанавливают графически или аналитически на огибающей эпюре моментов по ординатам М места теоретического обрыва стержней;

– определяют длину анкеровки обрываемых стержней W = Q /2 q_sw  + 5 d ³20 d, причем поперечная сила Q в месте теоретического обрыва стержня принимается соответствующей изгибающему моменту в этом сечении (рис. 5); здесь d -диаметр обрываемого стержня.

– в пролете допускается обрывать не более 50% расчетной площади сечения стержней, вычисленных по максимальному изгибающему моменту.

Рассмотрим сечения первого пролета. Арматура 2 Æ22 А-III + + 2Æ20 А-III c A_s = 13,88 см². Определяем момент, воспринимаемый сечением, для чего рассчитываем необх одимые параметры:

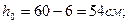
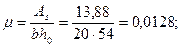
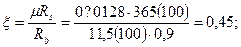
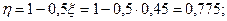
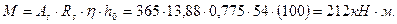
Арматура 2 Æ 20А-III с A_s = 7,6 см² доводится до опор, а стержни 2 Æ 20 A-III обрываются в пролете. Определяем момент, воспринимаемый сечением с арматурой 2 Æ 22 A-III:

;

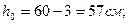
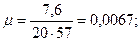
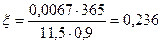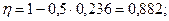
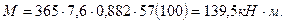
Графически определяем точки теоретического обрыва двух стержней Æ 20A-III. В первом сечении поперечная сила Q = 102 кН, во втором сечении Q = 55 кН. Интенсивность поперечного армирования в первом сечении при шагех омутов S = 20  см равна

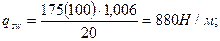
длина анкеровки W₁ = 102000/2х 880 + 5х 2 = 68 см > 20 = 40 см. Во втором сечении при шагех омутов S = 45 см q_sw = 391 Н/м; длина анкеровки W₂ = 55000/2х 391 + 5х 2 = 80 см.

Расчет эпюры арматуры для второго пролета аналогичный и поэтому здесь не приводится.

На первой промежуточной опоре слева принята арматура 2Æ12 A-III + 2Æ22A-IIIс A_s = 9,9 см²; μ = 0,009; ξ = 0,32; η = 0,84; М = 365х 9,9х 0,84х 54 (100) = 164 кНх м.

В месте теоретического обрыва остаются 2Æ12A-III с A_s = 2,6 см². Определяем момент, воспринимаемый сечением с этой арматурой. μ = 0,002; ξ = 0,07; η  = 0,965; М = 365х 2,26 х 0,965 х 57х (100) = 45,4 кН х м; поперечная сила в этом сечении Q = 140 кН; интенсивность поперечного армирования при шагех омутов S  =14 см q_sw = 1257 Н/см; длина анкеровки W₃ = 140000/2 х 1257 + 5 х 2,2 = 67 см > 20 х 2,2 = 44 см.

В такой же последовательности вычисляют значение W₄.

4.6. Расчет стыка сборных элементов ригеля

Рассматриваем вариант бетонированного стыка (рис. 6). В этом случае изгибающий момент на опоре воспринимается соединительными стержнями в верх ней растянутой зоне и бетоном, заполняющим полость между торцом ригелей и колонной.

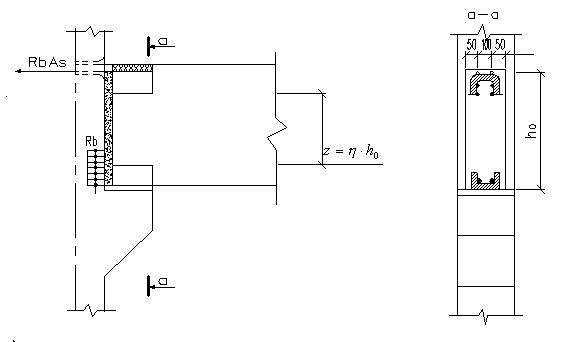
Рис. 6. К расчету бетонированного стыка

Принимаем бетон для замоноличивания класса В20;

R_b = 11,5 МПа: γ_b2 = 0,9; стыковые стержни из арматуры класса A-III; R_s  = 365 МПа.

Изгибающий момент ригеля по грани колонны М = 163,93 кН х м, рабочая высота сечения h₀ = 60 – 1,5 = 58,5 см.

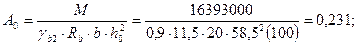
по табл. 3.1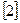нах одим соответствующее значение η = 0,868 и определяем площадь сечения стыковых стержней

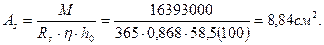
Принимаем арматуру 2 Æ 25 A-III с A_s = 9,82 см².

Длину сварных швов для приварки стыковых стержней с закладными деталями ригеля определяем следующим образом:

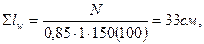
где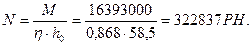

Коэффициент 1,3 вводим для обеспечения надежной работы сварных швов в случае перераспределения опорных моментов вследствие пластических деформаций.

При двух стыковых стержнях и двусторонних швах длина каждого шва (с учетом непровара) будет равна

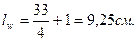
Конструктивное требование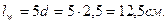

Принимаем .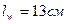

Закладная деталь ригеля приваривается к верх ним стержням каркаса при изготовлении арматурных каркасов. Сечение этой детали из условия прочности на растяжение:

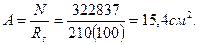
Конструктивно принята закладная деталь в виде гнутого швеллера из полосы δ = 8 мм, длиной 37 см; А = 0,8х 37 = 30 см²  > 15,4 см². Длина стыковых стержней складывается из размера сечения колонны, двух зазоров по 5 см между колонной и торцами ригелей и двух длин сварного шва l = 30 + 2х 5 + 2х 13 = 66 см.

ЛИТЕРАТУРА

1. СНиП 2.03.01-84. Бетонные и железобетонные конструкции/Госстрой СССР. – М.:ЦИТП Госстроя СССР, 1985.- 79 с.

2. Байков В.Н., Сигалов Э.Е.Железобетонные конструкции: Общий курс. Учебник для вузов. – 4-е изд., перераб. – М.: Стройиздат, 1985. – 728 с.

3. Попов Н.Н., Забегаев А.В. Проектирование и расчет железобетонных конструкций: Учеб. Пособие для строит. спец. вузов. – М.: Высшая школа, 1985. – 319 с.

4. Методические указания к курсовому проекту № 1 по дисциплине «Железобетонные конструкции» для специальности 1202 «Промышленное и гражданское строительство». Раздел 3. Сборные многопролетные ригели. – М., 1977(МИСИ им. В. В. Куйбышева).

5. Методические указания к первой части курса «Железобетонные и каменные конструкции» и задание к курсовому проекту № 1 для студентов 5 курса специальности «Промышленное и гражданское строительство»(1202). – М., 1982(ВЗИСИ).