Вопросы 3 и 4.Комплексная плоскость. Тригонометрическая и показательная формы комплексного числа

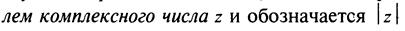
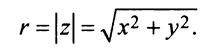
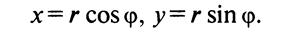
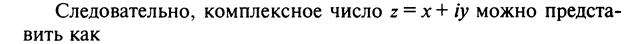
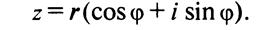
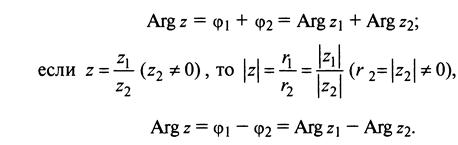
Пример 2.

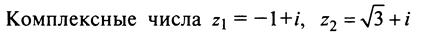
Решение: По формуле найдем модуль комплексного числа:

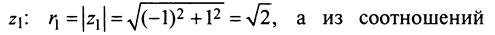
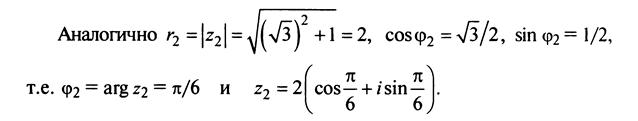
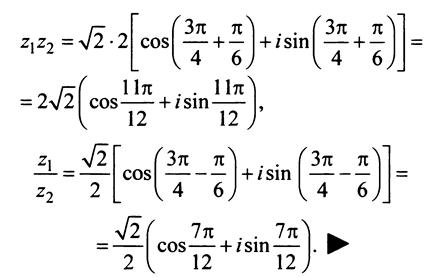
Так как в соответствии с формулами и при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень n, известную как формула Муавра:

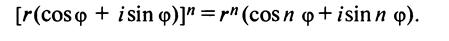
Пример 3, Решение: В примере 2 мы получили, что

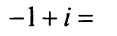
Поэтому по формуле Муавра:

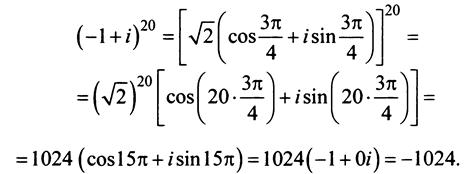
Обратимся к извлечению корня из комплексного числа.

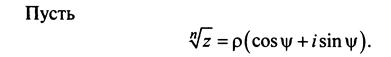
Тогда, используя определение корня и формулу Муавра, получим

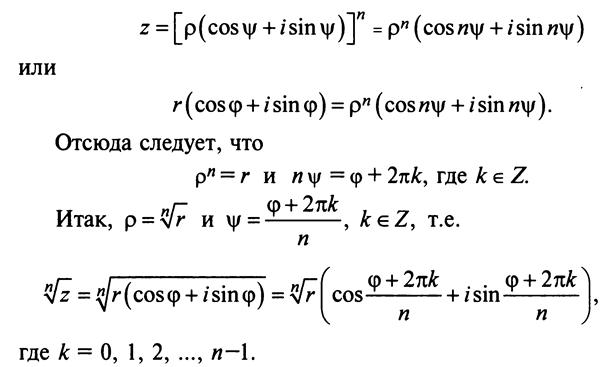
Пример 4.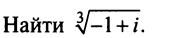

Решение. В примере 2 было получено:

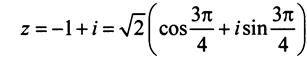
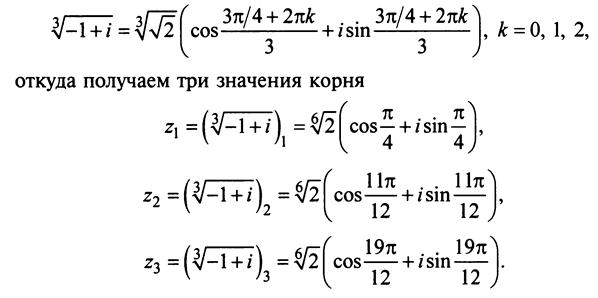
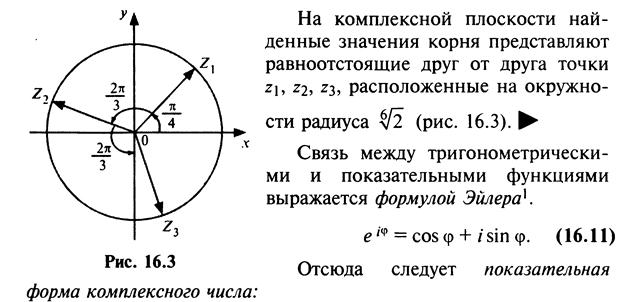
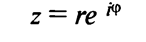
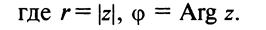
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.