Основные действия над комплексными числами в тригонометрической форме

· Сложение и вычитание комплексных чисел: в общем видене выполняется:

Умножение комплексных чисел: Произведение двух комплексных чисел есть такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

z₁z ₂ =r₁ (cosj ₁ +isinj ₁) r₂ (cosj ₂ +isinj ₂)= r₁r₂ [ cos (j ₁ +j ₂)+ isin (j ₁ +j ₂)];

· Деление комплексных чисел. Частное двух комплексных чисел есть такое комплексное число, модуль которого равен частному модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.

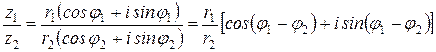
Например: Выполнить действия над комплексными числами в алгебраической форме и тригонометрической форме и сопоставить результаты: z ₁=-2+2 i; z ₂=1- i