Тригонометрическая форма комплексного числа

Геометрическое изображение комплексных чисел.

Всякое вещественное число геометрически можно изобразить точкой на вещественной оси и, обратно, каждой точке на оси соответствует вещественное число.

Всякое комплексное число z = а+ib можно изобразить на плоскости Оху в виде точки А (а, b) с координатами а и b. Обратно, каждой точке плоскости М (х, у) соответствует комплексное число z = х+iу.

Определение 1 Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменногоz.

Точкам плоскости комплексного переменного z, лежащим на оси Ох, соответствуют действительные числа (b =0).

Точкам плоскости комплексного переменного z, лежащим на оси Оу, соответствуют чисто мнимые числа (a =0).

Определение 2: На плоскости комплексного переменного z ось Оу называют мнимой осью, а ось Ох называют действительной осью.

Соединив точку А (а, b) с началом координат, получим вектор ОА, который принято считать геометрическим изображением комплексного числа z = а+ib.

Кроме записи z = а+ib употребляют z = х+iу.

Итак, геометрическим изображением комплексного числа z = а+ib является вектор, начало которого в точке (0; 0), а конец в точке (а; b). Любой вектор имеет две характеристики: модуль и направление.

Длина вектора, изображающего комплексное число z, называется модулем (абсолютной величиной) комплексного числа и обозначается r =| z.

Величина угла между положительным направлением действительной оси и вектором, изображающего комплексное число z, называется аргументом комплексного числа и обозначается j = argz.

Тогда а = r cos j, b=rsinj, а следовательно, комплексное число z можно представить в форме: а+ib = r cos j+ir sin j или z=r (cosj+isinj).

Определение 1: Выражение z=r (cosj+isinj), называется тригонометрической формой записи комплексного числа z = а + ib.

Величины r и j выражаются через а и b, очевидно, так:

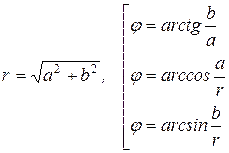
Аргумент комплексного числа считается положительным, если он отсчитывается от положительного направления оси Ох против часовой стрелки, и отрицательным при противоположном направлении отсчёта. Очевидно, что аргумент j определяется не однозначно, а с точностью до слагаемого 2pk, где k — любое целое число.

Замечание: Сопряженные комплексные числа а+ib и а - ib имеют равные модули, а их аргументы равны по абсолютной величине, но отличаются знаком.

Действительное число А так же может быть записано в тригонометрической форме комплексного числа, а именно:

A= | A |(cos 0 +isin 0) при А> 0,

A= | A |(cosp+isinp) при А< 0.

Модуль комплексного числа 0 равняется нулю 0: |0|=0. В качестве же аргумента нуля можно взять любой угол j. Действительно, для любого угла j имеет место равенство: 0=0(cosj+isinj).

Кроме алгебраической и тригонометрической форм комплексного числа имеет место показательная форма комплексного числа.

Определение 2: Выражение r·еⁱ^j, называется показательной (экспоненциальной) формой записи комплексного числа z = а + ib; r называется модулем, комплексного числа z, j — аргументом комплексного числа z.