Нормальное уравнение прямой
Дано: R = 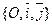 , , 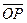 : : 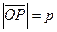 , , 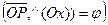 , l ' Р, l ^ , l ' Р, l ^ 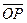 .
Найти уравнение l.
М Î l Û пр .
Найти уравнение l.
М Î l Û пр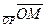 = р. Отсюда М Î l Û = р. Отсюда М Î l Û 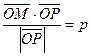 . Так как . Так как 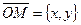 , , 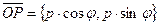 , то , то
| 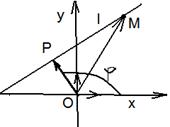 Рис. 22
Рис. 22
|
М Î l Û 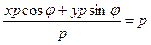 . Отсюда М Î l Û
. Отсюда М Î l Û 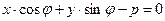 (30)
(30)
Уравнение (30) называется нормальное уравнение прямой.
Дано: R = 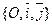 , l1: A1 x + B1 y + C1 = 0, l2: A2 x + B2 y + C2 = 0.
, l1: A1 x + B1 y + C1 = 0, l2: A2 x + B2 y + C2 = 0.
Найти один из углов 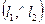 .
.
Замечание. Очевидно, достаточно найти только один из углов между прямыми.
Решение: 1-ый способ. Из уравнений l1 и l2 следует, что вектор 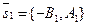 параллелен прямой l1 и вектор параллелен прямой l1 и вектор 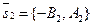 параллелен прямой l2. Следовательно, один из углов между l1 и l2 равен углу параллелен прямой l2. Следовательно, один из углов между l1 и l2 равен углу 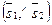 . Итак, . Итак,
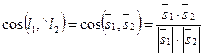 . (31) . (31)
| 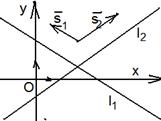 Рис 23
Рис 23
|
(Вывод формулы (31) можно проводить в любой аффинной системе координат). Воспользовавшись тем, что данная система координат прямоугольная, перепишем формулу (31) в координатах. Получим 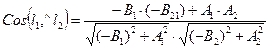 . Окончательно получим
. Окончательно получим
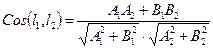 (32)
(32)
2-ой способ. Из уравнений l1 и l2 следует, что вектор 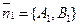 перпендикулярен прямой l1 и вектор перпендикулярен прямой l1 и вектор 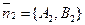 перпендикулярен прямой l2. Из свойства углов со взаимно перпендикулярными сторонами следует, что один из углов между l1 и l2 равен углу перпендикулярен прямой l2. Из свойства углов со взаимно перпендикулярными сторонами следует, что один из углов между l1 и l2 равен углу 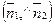 . Итак, . Итак,
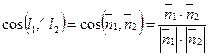 (33) (33)
| 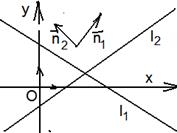 Рис. 24
Рис. 24
|
Переписав полученную формулу в координатах, получим
|
|
|
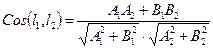 . (32)
. (32)
Замечание. Формулу (32) можно использовать только в том случае, когда прямые заданы общими уравнениями в прямоугольной системе координат.
Следствие. Две прямые перпендикулярны тогда и только тогда, когда А1А2 + В1В2 = 0 (33).
Задача. Дано. R = 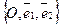 ,
, 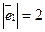 ,
, 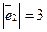 ,
, 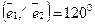 , l1: 3 х - 4 у + 11 = 0,
, l1: 3 х - 4 у + 11 = 0,
l2: 5 х + у + 8 = 0.
Найти 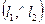 .
.
Решение. Используем формулу (31). В нашем случае 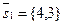 =
=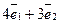 ,
, 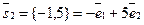 . Следовательно,
. Следовательно, 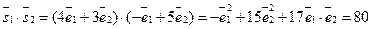 ;
; 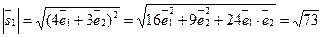 ,
, 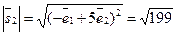 . Подставив в формулу (31), получим
. Подставив в формулу (31), получим 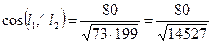 .
.
 2014-01-25
2014-01-25 753
753








