Дано: R = 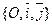 , l1: у = к1 × х + в1, l2: у = к2 × х + в2.
, l1: у = к1 × х + в1, l2: у = к2 × х + в2.
Найти ориентированный угол, на который нужно повернуть l1, чтобы она стала параллельной l2.
Решение. Из уравнений l1 и l2 следует, что 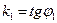 , , 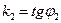 , где j1 и j2 – углы наклона прямых l1 и l2 к оси (О х). Обозначим q ориентированный угол между l1 и l2 . По свойству внешнего угла треугольника получим q = j2 - j1. Отсюда , где j1 и j2 – углы наклона прямых l1 и l2 к оси (О х). Обозначим q ориентированный угол между l1 и l2 . По свойству внешнего угла треугольника получим q = j2 - j1. Отсюда
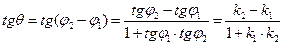 .
Итак, .
Итак, 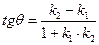 (34) (34)
| 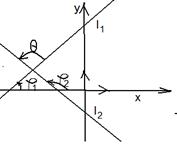 Рис. 25
Рис. 25
|
Следствие. Две наклонные прямые перпендикулярны тогда и только тогда, когда
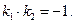 (35)
(35)
Задача. Дано: R = 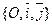 , l1: 3 х + 4 у +12 = 0, l2: 4 х - 7 у - 1 = 0.
, l1: 3 х + 4 у +12 = 0, l2: 4 х - 7 у - 1 = 0.
Найти тангенс угла между прямыми l1 и l2.
Решение. Используем формулу (34). Для этого нужно найти угловые коэффициенты данных прямых. Разрешая уравнения прямых относительно у, получим, что 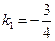 ,
, 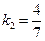 . Следовательно,
. Следовательно, 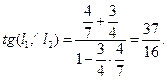
Задача. Дано: R = 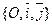 , l1: 3 х + 4 у +12 = 0, l2: 4 х + 3 у - 24 = 0.
, l1: 3 х + 4 у +12 = 0, l2: 4 х + 3 у - 24 = 0.
Найти уравнения биссектрис углов, образованных l1 и l2.
Решение. Если l3 и l4 – биссектрисы данных углов, то каждая из них проходит через точку А = l1 Ç l2. Координаты точки А найдём, решая систему уравнений 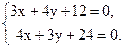 Получим А(
Получим А(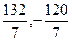 ).
).
По определению биссектрисы 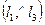 =
= 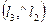 и
и 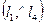 =
= 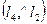 . Обозначим через к угловые коэффициенты l3 и l4. Используя формулу (34), получим
. Обозначим через к угловые коэффициенты l3 и l4. Используя формулу (34), получим
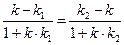 .
.
Так как 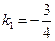 и
и 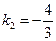 , то
, то 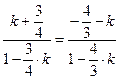 , или
, или 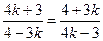 . Отсюда
. Отсюда 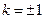 . Следовательно,
. Следовательно, 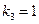 ,
, 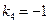 . Используя уравнение (27), получим
. Используя уравнение (27), получим
l3: (у + 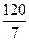 ) = 1×(х -
) = 1×(х - 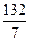 ). После упрощения l3: х - у - 36 =0.
). После упрощения l3: х - у - 36 =0.
Аналогично, l4: (у + 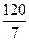 ) = -1×(х -
) = -1×(х - 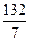 ). После упрощения l4: 7 х + 7 у - 12 =0.
). После упрощения l4: 7 х + 7 у - 12 =0.
 2014-01-25
2014-01-25 782
782








