Плоскость и прямая в прямоугольной системе координат
Дано: 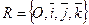 , М 0(х0, у0, z0), , М 0(х0, у0, z0), 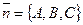 , , 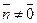 ,
П ' М0, П ^ ,
П ' М0, П ^ 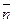 .
Найти уравнение П.
Решение. М Î П Û либо .
Найти уравнение П.
Решение. М Î П Û либо 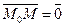 , либо , либо 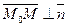 Û Û 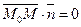 . Так как . Так как 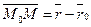 , то
М Î П Û , то
М Î П Û 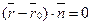 (47)
Это векторное уравнение данной плоскости. (47)
Это векторное уравнение данной плоскости.
| 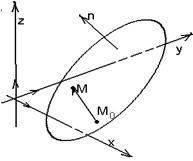 Рис. 33
Рис. 33
|
Переходя к координатам, получим А (х - х0) + В (у - у0) + С(z - z0) = 0/ (48)
Можно показать, что если плоскость задана в ПДСК общим уравнением (45), то вектор 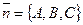 перпендикулярен этой плоскости.
перпендикулярен этой плоскости.
II.Угол между двумя плоскостями
Дано: 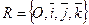 , П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0.
Найти один из углов между П1 и П2.
Решение. Из уравнений П1 и П2 следует, что , П1: А1х + В1у + С1z + D1 = 0, П2: А2х + В2у + С2z + D2 = 0.
Найти один из углов между П1 и П2.
Решение. Из уравнений П1 и П2 следует, что 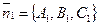 и и 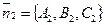 перпендикулярны плоскостям П1 и П2 соответственно. Если О – точка на линии пересечения П1 и П2, t1 и t2 лежат в плоскостях перпендикулярны плоскостям П1 и П2 соответственно. Если О – точка на линии пересечения П1 и П2, t1 и t2 лежат в плоскостях
| 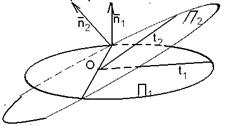 Рис. 34
Рис. 34
|
П1 и П2, проходят через точку О и перпендикулярны линии пересечения этих плоскостей (рис. 34), то 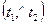 = (П1,
= (П1,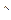 П2). Но по свойству углов со взаимно перпендикулярными сторонами
П2). Но по свойству углов со взаимно перпендикулярными сторонами 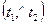 либо равен углу
либо равен углу 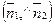 , либо дополняет его до 1800. И в том, и в другом случае
, либо дополняет его до 1800. И в том, и в другом случае 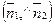 равен одному из углов между П1 и П2. Следовательно,
равен одному из углов между П1 и П2. Следовательно,
Cos((П1,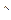 П2) =
П2) = 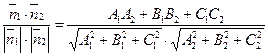 (49)
(49)
Из формулы (49) следует, что П1 ^ П2 Û 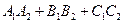 = 0.
= 0.
III.Угол между прямой и плоскостью
Дано: 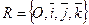 , П: Ах + Ву + Сz + D = 0,
t: , П: Ах + Ву + Сz + D = 0,
t: 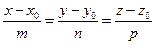 .
Найти один из углов между П и t.
Решение. Угол между прямой и плоскостью – это угол между прямой и её ортогональной проекцией на плоскость .
Найти один из углов между П и t.
Решение. Угол между прямой и плоскостью – это угол между прямой и её ортогональной проекцией на плоскость
| 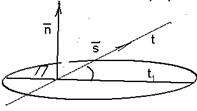 Рис. 35
Рис. 35
|
(рис. 35). Из уравнений прямой и плоскости вектор 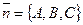 перпендикулярен плоскости П, а вектор
перпендикулярен плоскости П, а вектор 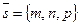 параллелен прямой t. Следовательно,
параллелен прямой t. Следовательно, 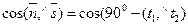 ). Отсюда следует, что
). Отсюда следует, что
sin(П,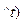 =
= 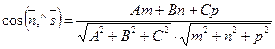 (50)
(50)
Из свойств векторов 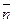 и
и 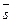 следует:
следует:
П // t Û 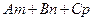 ; П ^ t Û
; П ^ t Û 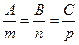 (51)
(51)
IV. Расстояние от точки до плоскости
 2014-01-25
2014-01-25 818
818








