Определение 5. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных различных точек есть постоянная величина (рис. 6).
Данные точки называются фокусами и обозначаются F1 и F2.
Данная постоянная величина обозначается 2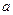 . Если êF1F2 ê= 2с,
то из свойств сторон треугольника F1F2М следует, что 2с > 2 . Если êF1F2 ê= 2с,
то из свойств сторон треугольника F1F2М следует, что 2с > 2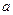 , т.е. с > , т.е. с > 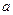 .
При изучении гиперболы нужно решить те же самые задачи, .
При изучении гиперболы нужно решить те же самые задачи,
| 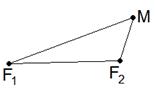 Рис. 6
Рис. 6
|
которые мы ставили для эллипса.
· Выбрав какую-либо систему координат, вывести уравнение гиперболы.
· Используя полученное уравнение, исследовать форму и свойства гиперболы.
Для вывода уравнения гиперболы выберем такую же каноническую систему координат, какая была использована для эллипса (рис. 2). В этой системе координат F1(-с, 0), F2 (с, 0). Пусть М (х, у). Тогда r1 = êF1Мê = 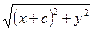 , r2 = êF2Мê=
, r2 = êF2Мê= 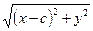 .
.
М Î гиперболе Û ú 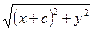 +
+ 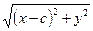 ú = 2 а, или
ú = 2 а, или
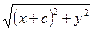 +
+ 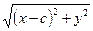 = ± 2 а (4)
= ± 2 а (4)
Уравнение (4) есть уравнение гиперболы. Упрощая его (проведите эти преобразования самостоятельно), получим
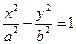 , где
, где 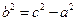 (5)
(5)
Так же как в случае эллипса можно показать, что уравнения (4) и (5) эквивалентны. Уравнение (5) называется каноническим уравнением гиперболы.
Исследуя уравнение (5), получаем следующие свойства гиперболы.
· 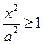 , т.е. х £ - , т.е. х £ -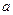 или х ³ или х ³ 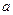 . Следовательно, вся гипербола лежит вне полосы, ограниченной прямыми х = ± . Следовательно, вся гипербола лежит вне полосы, ограниченной прямыми х = ± 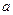 (рис.7).
· Гипербола пересекает ось (ОХ) в точках А1(- (рис.7).
· Гипербола пересекает ось (ОХ) в точках А1(-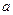 ,0), А2( ,0), А2(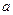 ,0). Отрезок А1А2 имеет длину 2 ,0). Отрезок А1А2 имеет длину 2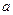 и называется действительной и называется действительной
| 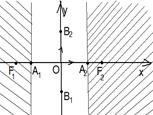 Рис. 7
Рис. 7
|
осью гиперболы. С осью (ОУ) гипербола не пересекается, но точки В1(0, -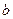 ) и В2(0,
) и В2(0, 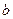 ) называются мнимыми вершинами гиперболы. Отрезок В1В2 имеет длину 2
) называются мнимыми вершинами гиперболы. Отрезок В1В2 имеет длину 2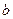 и называется мнимой осью гиперболы.
и называется мнимой осью гиперболы.
· Гипербола симметрична относительно координатных осей и начала координат. Следовательно, форму гиперболы достаточно исследовать только в первом координатном углу.
Пусть х ³ 0, у ³ 0. Тогда из уравнения (5) получим 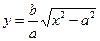 . Это уравнение той ветви гиперболы, которая лежит в первом координатном углу. Сравним эту ветвь гиперболы с лучом
. Это уравнение той ветви гиперболы, которая лежит в первом координатном углу. Сравним эту ветвь гиперболы с лучом 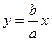 , лежащим в том же углу. При одном и том же значении х будет угип. < улуче, т.е. ветвь гиперболы лежит между осью (ОХ) и лучом (рис. 8). Пусть М и N точки на гиперболе и на
, лежащим в том же углу. При одном и том же значении х будет угип. < улуче, т.е. ветвь гиперболы лежит между осью (ОХ) и лучом (рис. 8). Пусть М и N точки на гиперболе и на
луче соответственно с одной и той же абсциссой.
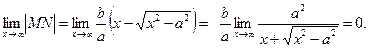 Итак, точки гиперболы неограниченно приближаются к точкам луча.
Используя симметрию относительно координатных осей, получим, что в остальных координатных углах гипербола неограниченно приближается к прямым
Итак, точки гиперболы неограниченно приближаются к точкам луча.
Используя симметрию относительно координатных осей, получим, что в остальных координатных углах гипербола неограниченно приближается к прямым 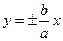 (рис. 9). (рис. 9).
| 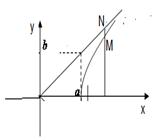 Рис. 8
Рис. 8
|
Определение 6. Прямые, которые в канонической системе координат задаются уравнениями 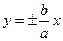 , называются асимптотами гиперболы.
Величина e = , называются асимптотами гиперболы.
Величина e = 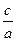 называется эксцентриситетом гиперболы. Очевидно, e > 1. называется эксцентриситетом гиперболы. Очевидно, e > 1.
| 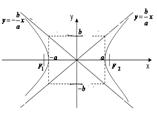 Рис. 9
Рис. 9
|
Определение 7. Прямые, которые в канонической системе координат имеют уравнения 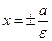 называются директрисами гиперболы.
называются директрисами гиперболы.
Теорема 4. Отношение расстояния от любой точки гиперболы до фокуса к расстоянию от этой же точки до соответствующей директрисы есть постоянная величина, равная эксцентриситету.
Доказательство этой теоремы аналогично доказательству теоремы 1.
Определение 8. Прямая называется касательной к гиперболе, если она имеет с гиперболой одну двукратную точку пересечения. Общая точка гиперболы и её касательной называется точкой касания.
Теорема 5. В любой точке гиперболы существует касательная к ней и только одна. Если гипербола задана уравнением (5) и точка касания М0(х0, у0), то касательная имеет уравнение
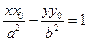 .
.
| Доказательство этой теоремы аналогично доказательству теоремы 2. Теорема 6. Если действительная ось гиперболы постоянна, то при e ® 1 гипербола стремится к паре лучей на оси (ОХ) с вершинами А1 и А2, если e ® ¥, то гипербола стремится к паре параллельных прямых х = ± а (рис. 10). Эта теорема доказывается аналогично теореме 3. | 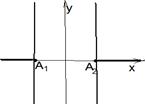 Рис. 10 Рис. 10
|
Замечание 1.. Если при выводе уравнения гиперболы через фокусы направить ось (ОУ) и постоянную, о которой идёт речь в определении, обозначить 2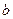 , то будет а 2 = с2 -
, то будет а 2 = с2 -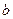 2 и уравнение гиперболы запишется
2 и уравнение гиперболы запишется 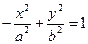 (6).
(6).
Гиперболы, заданные уравнениями (5) и (6) называются сопряжёнными. Сопряжённые гиперболы имеют они и те же асимптоты (рис. 11). Фокусы гиперболы (6): 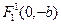 , , 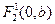 . Её эксцентриситет e = . Её эксцентриситет e = 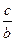 , директрисы у = , директрисы у = 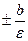 . .
| 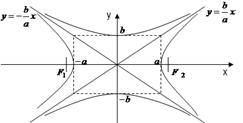 Рис. 11
Рис. 11
|
Замечание 2. Если центром гиперболы является точка С(х0, у0) и действительная ось параллельна оси (ОХ), то уравнение гиперболы 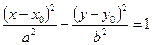 .
.
 2014-01-25
2014-01-25 779
779







