Плоскость в аффинной системе координат
Прямая и плоскость в пространстве
Уравнения прямой в пространстве были выведены в пункте 2.2. Это уравнения 141 - 181 и 19. там же было показано, как приводить общие уравнения прямой к каноническому виду в аффинной системе координат, и исследовано взаимное расположение двух прямых.
Дано:R = 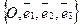 , М 0(х0, у0, z0), , М 0(х0, у0, z0), 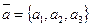 , , 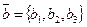 , ,  и и  неколлинеарны; П ' М0, П // неколлинеарны; П ' М0, П //  , П // , П //  . Найти условия, определяющие П (рис. 31). Решение. М Î П Û . Найти условия, определяющие П (рис. 31). Решение. М Î П Û 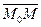 , ,  и и  компланарны. Так как компланарны. Так как  и и  неколлинеарны, то М Î П Û либо неколлинеарны, то М Î П Û либо | 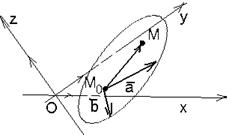 Рис. 31 Рис. 31 |
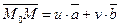 (u,v - любые действительные числа), либо определитель, составленный из координат этих векторов, равен нулю. Перепишем эти условия в координатах. Получим М Î П Û
(u,v - любые действительные числа), либо определитель, составленный из координат этих векторов, равен нулю. Перепишем эти условия в координатах. Получим М Î П Û 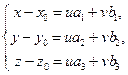 или М Î П Û
или М Î П Û 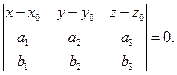 (39)
(39)
Получили два вида уравнений плоскости: уравнение (39) и 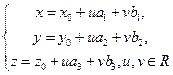 (40).
(40).
Уравнения (40) называются параметрическими уравнениями плоскости, проходящей через данную точку параллельно двум данным векторам.
Так как 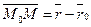 , где
, где 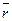 и
и 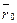 - радиусы-векторы точек М и М0 соответственно. Тогда уравнение
- радиусы-векторы точек М и М0 соответственно. Тогда уравнение 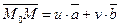 можно переписать
можно переписать 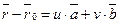 (41). Это векторное уравнение плоскости.
(41). Это векторное уравнение плоскости.
II.Уравнения плоскости, проходящей через три данные неколлинеарные точки
Дано: R = 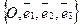 , М1 (х1, у1,z1), М2 (х2, у2, z2), М3 (x3, у3, z3), точки M1, M2, M3 не коллинеарные. П É í M1, M2, M3 ý.
, М1 (х1, у1,z1), М2 (х2, у2, z2), М3 (x3, у3, z3), точки M1, M2, M3 не коллинеарные. П É í M1, M2, M3 ý.
Найти уравнения П (рис. 32).
Решение. Так как M1, M2, M3 не коллинеарные, то векторы 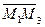 и и 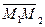 неколлинеарны. Используя уравнение (41), получим векторное уравнение плоскости, проходящей через три данные точки: неколлинеарны. Используя уравнение (41), получим векторное уравнение плоскости, проходящей через три данные точки: 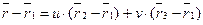 . (42) Используя (40) и (39), получим параметрические уравнения плоскости П и её уравнение в форме определителя. . (42) Используя (40) и (39), получим параметрические уравнения плоскости П и её уравнение в форме определителя. | 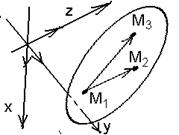 Рис. 32 Рис. 32 |
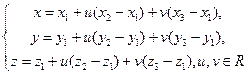 (43);
(43); 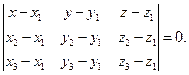 (44)
(44)
 2014-01-25
2014-01-25 1401
1401








