ОБРАЗЫ ВТОРОГО ПОРЯДКА
Цилиндрическая и сферическая системы координат в пространстве
Полярная система координат на плоскости
Различные системы координат на плоскости и в пространстве
VI. Расстояние между скрещивающимися прямыми
V. Расстояние от точки до прямой
2.7.3. Геометрический смысл неравенства Ах + Ву + Сz + D ³ 0 (£ 0, > 0, < 0)
4.1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ЛИНИЙ ВТОРОГО ПОРЯДКА
Определение 1. Окружностью с центром С и радиусом а называется множество точек плоскости, удалённых от точки С на расстояние а. Обозначение w = окр(С, а).
Если на плоскости зафиксирована ПДСК и С(х0,у0), то М Î w Û êСМê = а. Если М(х, у), то М Î w Û 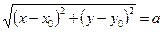 Û (х – х0)2 + (у – у0)2 = а 2. Следовательно, уравнение окружности в ПДСК есть (х – х0)2 + (у – у0)2 = а 2.
Û (х – х0)2 + (у – у0)2 = а 2. Следовательно, уравнение окружности в ПДСК есть (х – х0)2 + (у – у0)2 = а 2.
Если А(х1, у1) Î w, то уравнение касательной к w в точке А можно получить как уравнение прямой, проходящей через точку А перпендикулярно вектору 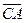 ={х1–х0,у1–у0}. Получим уравнение (х1 – х0)×(х – х0) + (у1 – у0)×(у – у0) = а 2.
={х1–х0,у1–у0}. Получим уравнение (х1 – х0)×(х – х0) + (у1 – у0)×(у – у0) = а 2.
4.1.2. ЭЛЛИПС
Определение 2. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных различных точек есть постоянная величина (рис. 1).
Данные точки называются фокусами и обозначаются F1 и F2.
Данная постоянная величина обозначается 2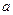 . Если êF1F2 ê= 2с,
то при . Если êF1F2 ê= 2с,
то при 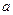 < с не существует ни одной точки М. При < с не существует ни одной точки М. При 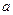 = с точки М заполняют отрезок F1F2. Поэтому для того, чтобы эллипс был
отличен от отрезка необходимо и достаточно, чтобы = с точки М заполняют отрезок F1F2. Поэтому для того, чтобы эллипс был
отличен от отрезка необходимо и достаточно, чтобы 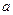 > с. > с.
| 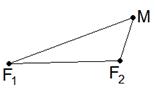 Рис. 1
Рис. 1
|
Поставим задачи:
· Выбрав какую-либо систему координат, вывести уравнение эллипса.
· Используя полученное уравнение, исследовать форму и свойства эллипса.
Так как в определении эллипса используется расстояние между точками, то систему координат лучше выбрать прямоугольную. Так как все точки эллипса связаны с фокусами, то за начало координат лучше выбрать середину отрезка F1F2. Ось (ОХ) направим через фокусы в направлении от F1 к F2 (рис. 2). Выбранная система координат называется
канонической системой координат для эллипса. В этой системе
координат F1(-с, 0), F2 (с, 0). Пусть М (х, у). Тогда
r1 = êF1Мê = 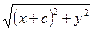 , r2 = êF2Мê= , r2 = êF2Мê= 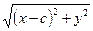 .
М Î эллипсу Û r1 + r2 = 2 а. Следовательно,
М Î эллипсу Û .
М Î эллипсу Û r1 + r2 = 2 а. Следовательно,
М Î эллипсу Û 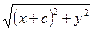 + + 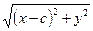 = 2 а (1)
Уравнение (1) есть уравнение эллипса. Упростим его. Для этого = 2 а (1)
Уравнение (1) есть уравнение эллипса. Упростим его. Для этого
| 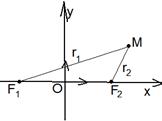 Рис. 2
Рис. 2
|
уединим один из корней и возведём в квадрат.
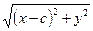 = 2 а -
= 2 а - 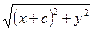 ,
,
х2 – 2сх + с2 + у2 = 4 а 2 – 4 а 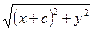 + х2 + 2сх + с2 + у2
+ х2 + 2сх + с2 + у2
а 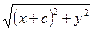 = а 2 + сх.
= а 2 + сх.
Ещё раз возведя в квадрат, получим
а 2х2 + 2 а 2сх + а 2с2 + а 2у2 = а 4 + 2 а 2сх + с2х2,
(а 2 – с2)х2 + а 2у2 = а 2(а 2 – с2).
Так как 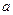 > с, то можно обозначить а 2 – с2 = в2. Последнее уравнение запишется
> с, то можно обозначить а 2 – с2 = в2. Последнее уравнение запишется
в 2х2 + а 2у2 = а 2 в2. Разделив на = а 2 в2, получим
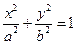 (2)
(2)
Итак, уравнение (1) преобразовано в уравнение (2). Но при этом два раза применяли возведение в квадрат. Следовательно, нужно проверить, что уравнения (1) и (2) эквивалентны. Для этого достаточно показать, что, если координаты (х, у) удовлетворяют уравнению (2), то они удовлетворяют и уравнению (1).
Пусть (х, у) удовлетворяют уравнению (2). Тогда 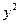 =
= 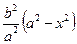 . Подставив у2 в выражение для r1, получим r1 =
. Подставив у2 в выражение для r1, получим r1 = 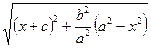 =
= 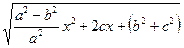 = =
= = 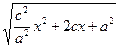 =
= 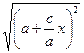 =
= 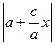 =
= 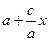 (Из уравнения (2) следует, что - а £ х £ а. Так как
(Из уравнения (2) следует, что - а £ х £ а. Так как 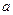 > с, то
> с, то 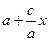 > 0). Аналогично получим, что r2 =
> 0). Аналогично получим, что r2 = 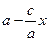 . Следовательно, r1 + r2 = 2
. Следовательно, r1 + r2 = 2 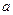 , но это значит, что точка М(х, у) лежит на эллипсе. Итак, уравнения (1) и (2) эквивалентны. Уравнение (2) называется каноническим уравнением эллипса.
, но это значит, что точка М(х, у) лежит на эллипсе. Итак, уравнения (1) и (2) эквивалентны. Уравнение (2) называется каноническим уравнением эллипса.
Будем исследовать эллипс, используя уравнение (2). Из него следует:
· 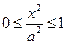 , т.е. , т.е. 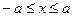 ;
· эллипс пересекает ось (ОХ) в точках А1(- ;
· эллипс пересекает ось (ОХ) в точках А1(-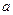 ,0) и А2( ,0) и А2(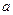 , 0);
· , 0);
· 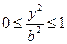 , т.е. , т.е. 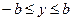 ;
· эллипс пересекает ось (ОУ) в точках В1(0, - ;
· эллипс пересекает ось (ОУ) в точках В1(0, - ) и ) и
| 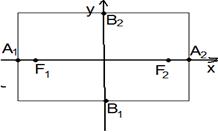 Рис. 3
Рис. 3
|
В2(0,  );
);
· эллипс вписан в прямоугольник, стороны которого параллельны осям координат и проходят через точки А1, А2, В1, В2 (рис. 3);
· эллипс симметричен относительно осей координат и относительно начала координат;
· в первом координатном углу при увеличении х от нуля до а координата у убывает от нуля до  (рис. 4).
· длины отрезков А1А2 и В1В2 равны 2 а и 2 (рис. 4).
· длины отрезков А1А2 и В1В2 равны 2 а и 2 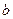 соответственно. Эти отрезки называются большой и малой осью эллипса соответственно. Точки А1, А2, В1, В2 называются вершинами эллипса. Фокусы
эллипса лежат на его большой оси между вершинами. соответственно. Эти отрезки называются большой и малой осью эллипса соответственно. Точки А1, А2, В1, В2 называются вершинами эллипса. Фокусы
эллипса лежат на его большой оси между вершинами.
|  Рис.4
Рис.4
|
Величина e = 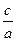 называется эксцентриситетом эллипса. Очевидно, 0 < e < 1.
называется эксцентриситетом эллипса. Очевидно, 0 < e < 1.
Определение 3. Прямые, которые в канонической системе координат имеют уравнения 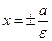 называются директрисами эллипса.
называются директрисами эллипса.
Так как e < 1, то эллипс лежит между своими директрисами (рис. 5).
Фокус F1(-с, 0) и директриса 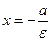 , а так же фокус F2(с, 0) и директриса
, а так же фокус F2(с, 0) и директриса 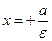 называются соответствующими.
называются соответствующими.
Теорема 1. Отношение расстояния от любой точки эллипса до фокуса к расстоянию от этой же точки до соответствующей директрисы есть постоянная величина, равная эксцентриситету.
Доказательство. êF1М ê= 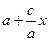 = а + eх, êМК1ê= = а + eх, êМК1ê= 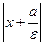 =
= =
= 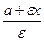 . Следовательно, êF1М ê: êМК1ê = e (рис. 5).
Аналогично, êF2М ê: êМК2ê = e.
(Здесь МК1 и МК2 - перпендикуляры, опущенные из точки М на директрисы р1 и р2 соответственно.) . Следовательно, êF1М ê: êМК1ê = e (рис. 5).
Аналогично, êF2М ê: êМК2ê = e.
(Здесь МК1 и МК2 - перпендикуляры, опущенные из точки М на директрисы р1 и р2 соответственно.)
| 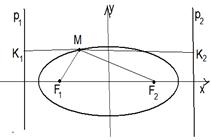 Рис. 5
Рис. 5
|
Определение 4. Прямая называется касательной к эллипсу, если она имеет с эллипсом одну двукратную точку пересечения. Общая точка эллипса и его касательной называется точкой касания.
Теорема 2. В любой точке эллипса существует касательная к нему и только одна. Если эллипс задан уравнением (2) и точка касания М0(х0, у0), то касательная имеет уравнение
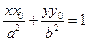 (3).
(3).
Доказательство. Если М0(х0, у0) – любая точка эллипса, то 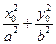 = 1 (*). Пусть р – любая прямая, проходящая через точку М0. Тогда уравнения р будут х = х0 + mt, у = у0 + nt, где {m, n} – координаты направляющего вектора прямой р. Для того чтобы найти уравнение касательной, достаточно найти m и n. Координаты точки пересечения эллипса и прямой р должны удовлетворять системе
= 1 (*). Пусть р – любая прямая, проходящая через точку М0. Тогда уравнения р будут х = х0 + mt, у = у0 + nt, где {m, n} – координаты направляющего вектора прямой р. Для того чтобы найти уравнение касательной, достаточно найти m и n. Координаты точки пересечения эллипса и прямой р должны удовлетворять системе 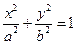 , х = х0 + mt, у = у0 + nt.
, х = х0 + mt, у = у0 + nt.
Подставляя х и у в первое уравнение системы, получаем 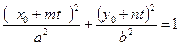 . Отсюда
. Отсюда
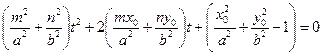 . Используя (*), получим
. Используя (*), получим 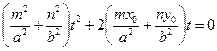 . Так как t = 0 является решением полученного уравнения, то для существования уравнения касательной необходимо и достаточно, чтобы второй его корень тоже был равен нулю, т.е. должно быть
. Так как t = 0 является решением полученного уравнения, то для существования уравнения касательной необходимо и достаточно, чтобы второй его корень тоже был равен нулю, т.е. должно быть 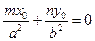 . Все решения этого уравнения пропорциональны решению
. Все решения этого уравнения пропорциональны решению 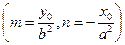 . Так как все эти решения определяют пропорциональные векторы, то искомая касательная существует и только одна. Найдём её уравнение, используя каноническое уравнение прямой, проходящей через данную точку параллельно данному вектору. Получим
. Так как все эти решения определяют пропорциональные векторы, то искомая касательная существует и только одна. Найдём её уравнение, используя каноническое уравнение прямой, проходящей через данную точку параллельно данному вектору. Получим 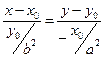 . Преобразуя это уравнение и используя (*), получим уравнение
. Преобразуя это уравнение и используя (*), получим уравнение 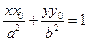 .
.
Теорема 3. Если большая ось эллипса постоянна, то при e ® 0 эллипс стремится к окружности, если e ® 1, то эллипс стремится к своей большой оси (т.е. к отрезку А1А2).
Доказательство. Так как 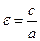 и
и 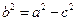 , то при постоянном а с уменьшением e уменьшается с, а
, то при постоянном а с уменьшением e уменьшается с, а  увеличивается. Если e ® 0, то
увеличивается. Если e ® 0, то  ® а, т.е. эллипс стремится к окружности. При этом фокусы сближаются и стремятся к центру окружности. Следовательно, окружность есть предельное положение эллипса. Если e ® 1, то с ® а,
® а, т.е. эллипс стремится к окружности. При этом фокусы сближаются и стремятся к центру окружности. Следовательно, окружность есть предельное положение эллипса. Если e ® 1, то с ® а, 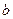 ® 0, Фокусы стремятся к вершинам большой оси, а сам эллипс стремится к отрезку А1А2.
® 0, Фокусы стремятся к вершинам большой оси, а сам эллипс стремится к отрезку А1А2.
Замечание 1. Если при выводе уравнения эллипса через фокусы направить ось (ОУ) и постоянную, о которой идёт речь в определении, обозначить 2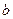 , то будет
, то будет 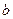 > с, а 2 =
> с, а 2 = 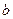 2 – с2 и уравнение эллипса будет такого же вида
2 – с2 и уравнение эллипса будет такого же вида 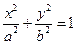 , но
, но 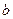 > а.
> а.
Замечание 2. Если центром эллипса является точка М(х0, у0), но оси его параллельны координатным осям, то уравнение эллипса будет 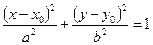 .
.
 2014-01-25
2014-01-25 835
835








