Плоскость и прямая в пространстве

Любая плоскость определяется линейным уравнением

Ах + Ву + Сz + D = 0, А² + В²+ C² ≠ 0, (20)

которое называется общим уравнением плоскости (здесь А, В, С можно рассматривать как координаты вектора нормали 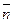, перпендикулярного плоскости (20), нормального вектора плоскости).

Уравнение

A (x – x₀) + B (y – y₀) + C (z – z₀) = 0 (21)

представляет собой уравнение плоскости, перпендикулярной вектору нормали 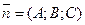и проходящий через точку М ₀(х ₀; у ₀; z ₀).

Уравнение плоскости, проходящей через точки М (х ₁; у ₁; z ₁), N (х ₂; у ₂; z ₂) и L (x ₃; y ₃; z ₃) имеет вид:

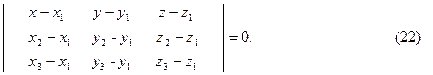
Частным случаем этой формулы является уравнение плоскости в отрезках:

здесь a, b, c – абсцисса, ордината и аппликата точек пересечения плоскости с осями Ох, Оу, Оz.

Условия параллельности и перпендикулярности двух плоскостей соответственно имеют вид:

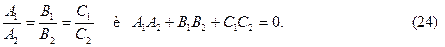
Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе:

Если прямая параллельна вектору 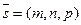(называемому направляющим вектором) и проходит через точку М₀ (х₀; у₀; z₀), то ее уравнение имеет вид:

Условия параллельности и перпендикулярности двух прямых, заданных уравнениями

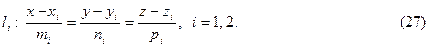
в пространстве соответственно имеют вид:

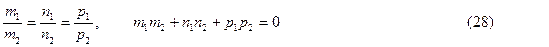
Условие пересечения двух прямых l ₁ и l ₂ в прстранстве записывается в виде:

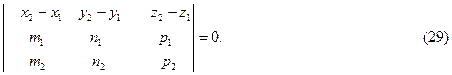
Условия параллельности прямой (26) и плоскости (20) соответственно имеют вид:

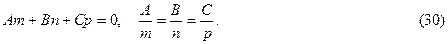
Расстояние от точки М₀ (х₀; у₀; z₀) до плоскости, заданной уравнением (20), находится по формуле: