1. Коммутативность: 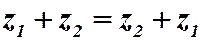 .
.
2. Ассоциативность сложения: 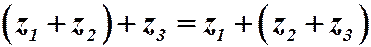 .
.
3. Для любых комплексных чисел 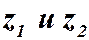 существует комплексное число z:
существует комплексное число z: 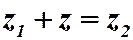 Это число
Это число 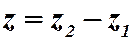 называется разностью чисел
называется разностью чисел 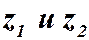 .
.
4. Коммутативность умножения: 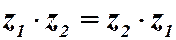 .
.
5. Ассоциативность умножения: 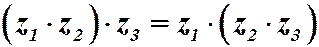 .
.
6. Дистрибутивность: 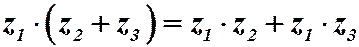 .
.
7. Вывод: Сложение и умножение комплексных чисел подчиняются тем же законам, что и сложение, и умножение действительных чисел. И вообще, множество действительных чисел – это частный случай комплексных чисел 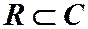 .
.
Пример 2.2. Найти сумму и произведение комплексных чисел: 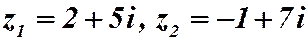
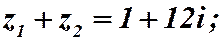
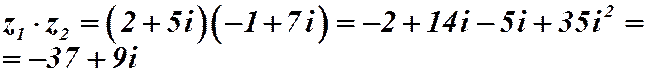 Пример 2.3
Пример 2.3 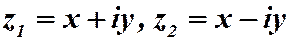 ;
;
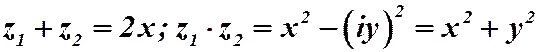 .
.
Определение 2.2. Числа,  отличающиеся только знаком мнимой части, называются сопряженными комплексными числами и обозначаются
отличающиеся только знаком мнимой части, называются сопряженными комплексными числами и обозначаются 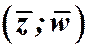 .
.
Пример 2.3 показывает, что сумма 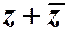 - есть число действительное,
- есть число действительное, 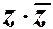 - есть число действительное и неотрицательное.
- есть число действительное и неотрицательное.
Пример 2.4. Даны комплексные числа 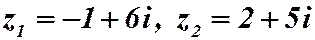 . Найти разность и их частное
. Найти разность и их частное 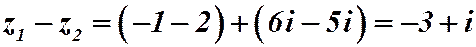
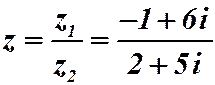 Умножим числитель и знаменатель на комплексное число, сопряженное знаменателю:
Умножим числитель и знаменатель на комплексное число, сопряженное знаменателю:
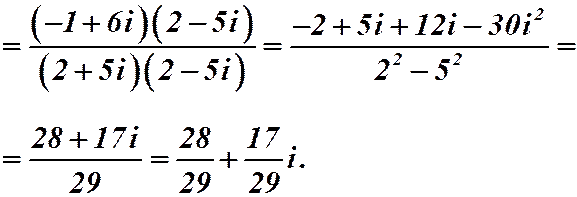
 2014-01-25
2014-01-25 868
868








