Операции над комплексными числами
Пусть даны два комплексных числа:
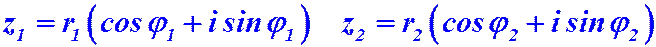 1) Умножение. При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются, то есть:
1) Умножение. При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются, то есть:
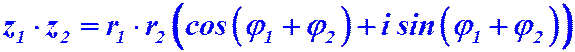 .
.
2) Деление. При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются, то есть:
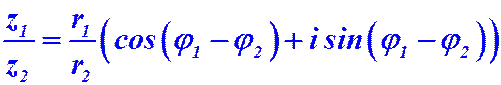 .
.
Пример 2.9. Записать число в тригонометрической форме: 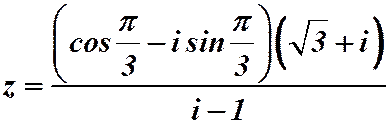 .
.
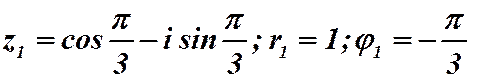 .
.
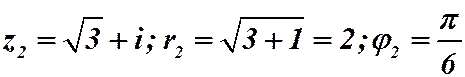 , т.к.
, т.к.
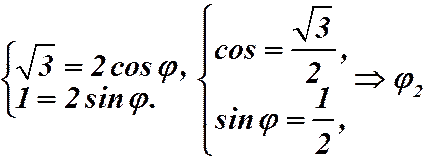
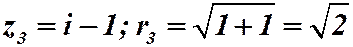 .
.
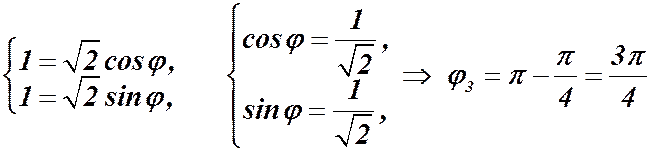
так как наше число во II квадранте. Получаем:
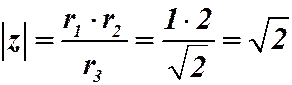 - это аргумент.
- это аргумент.  .
.
Ответ: 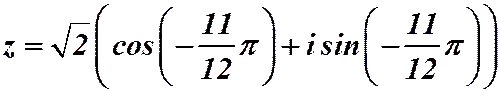 .
.
3)Возведение в степень. При возведении в степень комплексного числа, заданного в тригонометрической форме, модуль числа нужно возвести в п-ю степень, а аргумент умножить на число п, то есть:
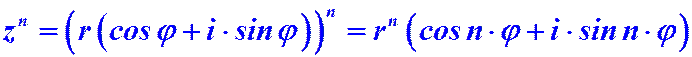 формула Муавра.
формула Муавра.
Пример 2.10. 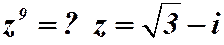 .
.
Решение: 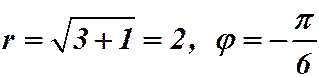 ,
,
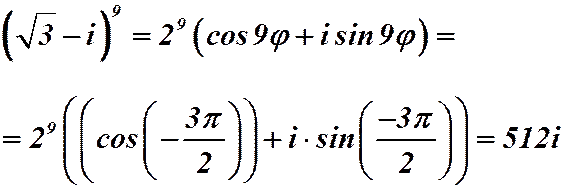
Определение 2.5. Число 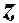 называется корнем степени
называется корнем степени 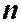 ( где
( где 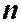 - натуральное число, большее или равное двум) из числа
- натуральное число, большее или равное двум) из числа 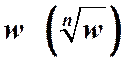 , если
, если 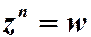 .
.
Рассмотрим следующие случаи:
1) Если 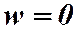 , тогда
, тогда 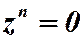 и
и 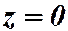 имеет единственное решение.
имеет единственное решение.
2) Если 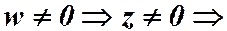 можно
можно 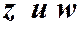 представить в тригонометрической форме и
представить в тригонометрической форме и 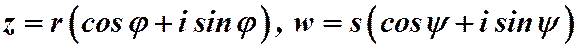 .
.
Тогда уравнение 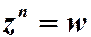 примет вид:
примет вид: 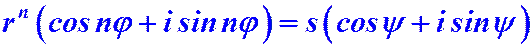 . Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются слагаемым, кратным
. Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются слагаемым, кратным 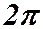 . То есть,
. То есть, 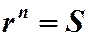 или
или 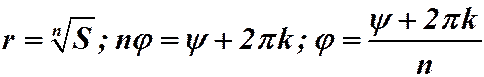 . Итак, все решения (имеется ровно
. Итак, все решения (имеется ровно 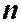 значений) уравнения
значений) уравнения 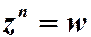 , которые могут быть записаны в виде:
, которые могут быть записаны в виде: 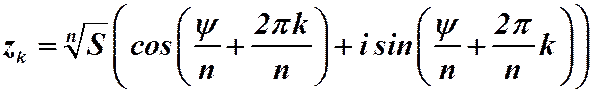 , где k=0,1,2,…,(
, где k=0,1,2,…,(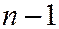 ).
).
Пример 2.11. Найти все значения 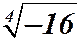 .
.
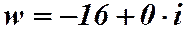 запишем в тригонометрической форме:
запишем в тригонометрической форме: 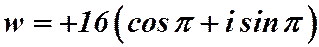 . По формуле:
. По формуле:
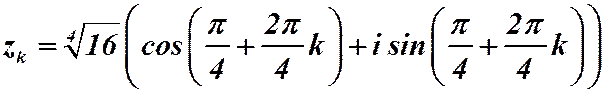 ,
, 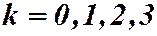 .
.
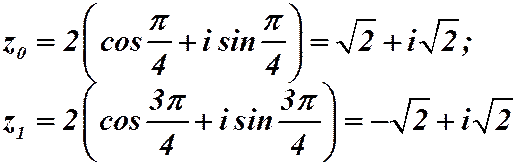 ,
,
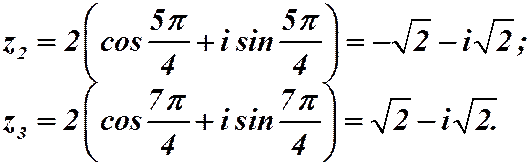
 2014-01-25
2014-01-25 737
737








