Комплексное число

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Запрос «Мнимая величина» перенаправляется сюда; см. также другие значения.

Запрос «Re» перенаправляется сюда; см. также другие значения.

Запрос «Im» перенаправляется сюда; см. также другие значения.

Ко́мпле́ксные^[1] чи́сла (устар. Мнимые числа ^[2]), — расширение множества вещественных чисел, обычно обозначается 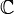. Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица^[3].

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.