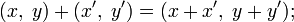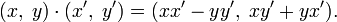Стандартная модель

Определения

Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z ² + 1 имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел , как и любые другие конструкции поля разложения многочлена z ² + 1.

Комплексное число z можно определить как упорядоченную пару вещественных чисел (x, y). Введём операции сложения и умножения таких пар следующим образом:

Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида 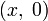, причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой 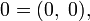единица — 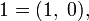а мнимая единица — 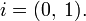На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен 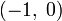, то есть − 1.

Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.