2014-01-25
1825
Определение. Корнем n-ой степени из комплексного числа z называется комплексное число, n- ая степень которого равна z.
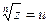, если 
.
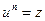Получим правило извлечения корня n -ой степени из комплексного числа, записанного в тригонометрической форме, пользуясь определением. Итак, пусть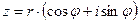 
. Найдем 
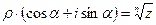. Имеем по определению 
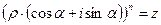, откуда по формуле Муавра получим 
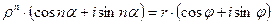. Так модуль комплексного числа определяется однозначно, а аргумент – с точностью до слагаемого, кратного 
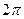, то 
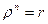и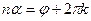 
. Таким образом, 
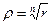, а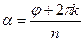 
.
Итак,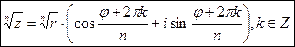 
.
Пример. Найти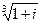 
. Запишем число в тригонометрической форме 
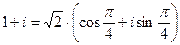. Теперь применим формулу 
.
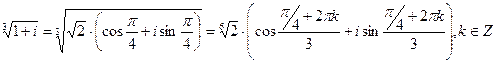Если k= 0, то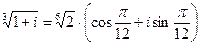 
. Если k= 1, то 
.
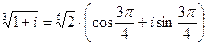Если k= 2, то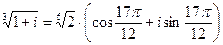 
. Если k= 3, то .
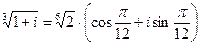Заметим, что при извлечении корня третьей степени получили три различных комплексных числа. Справедлива следующая теорема.
Лемма. Существует ровно n различных корней n -ой степени из комплексного числа. Для получения этих значений достаточно применить формулу для вычисления корня при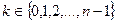 
.
Доказательство. Самостоятельно.
Интересным свойством обладают комплексные корни n-ой степени из единицы. Попробуем получить это свойство, рассматривая пример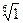 
. Запишем единицу в тригонометрической форме и применим формулу для вычисления корней:
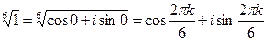. Получим шесть различных значений. Изобразим их на комплексной плоскости.
Итак, полученные значения оказались вершинами правильного шестиугольника, вписанного в единичную окружность, причем одна из вершин – в точке (1,0).
Это утверждение можно обобщить. Попробуйте сделать это самостоятельно.
Определение. Корень n -ой степени из единицы называется первообразным корнем, если все корни представимы в виде его степени.
