Понятие корреляционно-регрессионного анализа

Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов.

В наиболее общем виде задача изучения взаимосвязей факторов состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ, объединенные в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнение при интерпретации результатов и др.

Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками и оценке факторов, оказывающих наибольшее влияние на результативный признак. Показатели, используемые для оценки тесноты связи, приведены в п. 9.3, 9.5, 9.6.

Задачи регрессионного анализа лежат в сфере установления формы зависимости, определении функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной. Найти уравнение регрессии – значит по эмпирическим (фактическим) данным описать изменения взаимно коррелируемых величин.

Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х не учитывать, т.е. абстрагироваться от них. Уравнение регрессии называют теоретической линией регрессии, а рассчитанные по нему значения результативного признака - теоретическими. Теоретические значения результативного признака обычно обозначаются 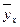(читается: «игрек, выровненный по икс») и рассматривается как функция от х, т.е. 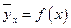. Иногда для простоты записи вместо 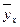пишут 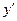или.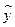

Для аналитической связи между х и у используются следующие простые виды уравнений: 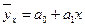(прямая); 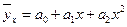(парабола второго порядка); 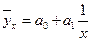(гипербола); 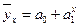(показательная или экспоненциальная функция); 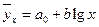(логарифмическая фу-

нкция) и др. Обычно зависимость, выраженную уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными.

Различают парную и множественную (многофакторную) корреляцию (см. табл. 9.1), а, следовательно, и, парную и множественную регрессии.

Корреляционно-регрессионный анализ, в частности многофакторный корреляционный анализ, состоит из нескольких этапов.

На первом этапе определяются факторы, оказывающие воздействие на изучаемый показатель, и отбираются наиболее существенные. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. При отборе факторов придерживаются требований, представленных на рис. 9.3.

Рис. 9.3. Перечень основных требований, учитываемых при отборе факторов, оказывающих воздействие на изучаемый показатель

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. Собранная исходная информация должна быть проверена на точность (достоверность), однородность и соответствие закону нормального распределения. Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации. Если вариация выше 33%, то это говорит о неоднородности информации и ее необходимо исключить или отбросить нетипичные наблюдения.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию: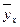 = a₀+a₁x₁+a₂x₂+ a₃x₃+…+a_пx_п. Если связь между функцией и исследуемым и показателями носит криволинейный характер, то может быть использована степенная функция: 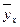= b₀ * x₁^b1 * x₂^b2 *…*x_п^bп.

На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. Рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, множественные коэффициенты корреляции и др.

На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение. Для этого дается оценка коэффициентов регрессии, коэффициентов эластичности и бетта-коэффициентов.

Одним из основным условий применения и ограничении корреляционно-регрессионного метода является наличие данных по достаточно большой совокупности явлений. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.