Помимо степенных средних в статистике связи также используются структурные средние: мода, медиана, квартиль, дециль, перцентиль.
Являясь важнейшей обобщающей характеристикой вариационного ряда средняя величина характеризует центр распределения. Однако значение средней может не совпадать ни с одной из реально существующих вариант, например, средний тарифный разряд равен 3,6, хотя разряд рабочего не может быть дробным числом. Поэтому наряду со средней для анализа рядов распределения целесообразно применять значения конкретных вариант, которые в упорядоченном ряду занимают определенное положение. К таким значениям относятся мода и медиана, называемые описательными или структурными характеристиками рядов распределения.
Особенно ценны эти показатели для характеристики небольших по численности совокупностей. Совместно используются средняя арифметическая, мода и медиана при анализе симметрии ряда распределения.
Мода – это вариант, обладающий наибольшей частотой или частостью. Этот показатель применяется в тех случаях, когда необходимо охарактеризовать наиболее часто встречающееся значение признака, наиболее распространенный вид услуг связи, преобладающую форму организации труда, типичную конфигурации информационных и телекоммуникационных сетей. В интервальном ряду с равными интервалами мода рассчитывается на основе интерполяции модального интервала по следующей формуле:
|
|
|
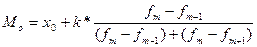 ,
,
где: х0 – начальная граница модального интервала; k – модальный интервал; fm-1, fm, fm+1 – частоты интервалов предшествующего модальному, модального и следующего за модальным.
В дискретных рядах моду находят по наибольшей частоте.
Медианой является вариант, делящий численность вариационного ряда на две равные части. Этот вариант расположен в центре ранжированного ряда, при этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой больше.
Для определения медианы в дискретных рядах необходимо придать всем единицам ряда порядковые номера. В рядах с нечетным количеством членов ряда медианой является член ряда, имеющий порядковый номер середины ряда (n+1)/2. Например, в ряду с количеством членов ряда 101 номер медианного показателя 51-й: (101+1)/2=51. В рядах с четным числом членов ряда медианой является среднее значение двух вариантов, имеющих номера n/2 и (n+1)/2. Так, если в ряду 100 членов ряда, то медианой является вариант, находящийся между 50-м и 51-м членами ряда. Однако в рядах с большим числом единиц совокупности и незначительным различием в значениях рядом стоящих вариантов медианой обычно считается вариант с порядковым номером n/2.
|
|
|
Нахождению медианы в интервальном ряду предшествует определение медианного интервала, накопленная (кумулятивная) частота которого равна или превышает полусумму всех частот ряда. Затем медиана рассчитывается по формуле
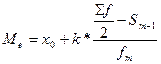 ,
,
где: х0 – начальная граница медианного интервала; k – медианный интервал; Sf – сумма накопленных частот (численность) ряда; Sm-1 – сумма накопленных частот интервалов, предшествующих медианному; fm – частота медианного интервала.
По аналогии с нахождением медианы в вариационных рядах можно найти значение признака у любой ранжированной в определенном порядке единицы, например, у единиц, делящих ряд на четыре равные части, десять или сто частей.
Квартили – это значения признака, делящие ранжированную совокупность на четыре равновеликие части. Это означает, что 25% единиц совокупности будут меньше по величине Q1, 25% единиц заключены между Q1 и Q2, 25% – между Q2 и Q3, остальные 25% превосходят Q3. Вторым квартилем является медиана. Для расчета квартилей в интервальном вариационном ряду применяют формулы:
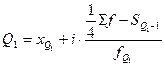 ,
, 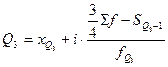 ,
,
где: 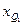 ,
, 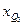 – нижняя граница интервала, содержащего первый, третий квартиль (интервал определяется по накопленной частоте, первой превышающей 25%, 75%);
– нижняя граница интервала, содержащего первый, третий квартиль (интервал определяется по накопленной частоте, первой превышающей 25%, 75%);
i – величина интервала; 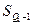 ,
, 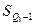 – накопленная частота интервала, предшествующего интервалу, содержащему первый, третий квартиль;
– накопленная частота интервала, предшествующего интервалу, содержащему первый, третий квартиль;
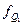 ,
, 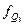 – частота интервала, содержащего первый, третий квартиль.
– частота интервала, содержащего первый, третий квартиль.
Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль (d1) делит совокупность в соотношении 1/10 к 9/10, второй дециль (d2) – в соотношении 2/10 к 8/10 и т.д. Расчет децилей осуществляется по той же схеме, что и медиана и квартили:
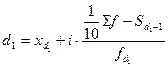 ,
, 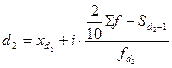 .
.
Значения признака, делящие ряд на сто частей, называются перцентилями.
Использование в анализе рядов распределения единиц по социально и технико-экономическим параметрам отрасли связи и информатизации структурных средних позволяет более глубоко и детально охарактеризовать изучаемую совокупность.
Соотношение моды, медианы и средней арифметической указывает на характер распределения и его асимметрию. В симметричном ряду распределения все три характеристики совпадают: 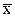 = Мо = Ме. Чем больше расхождение между ними, тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней не более трех раз превышает разность между медианой и средней:
= Мо = Ме. Чем больше расхождение между ними, тем более асимметричен ряд. Для умеренно асимметричных рядов разность между модой и средней не более трех раз превышает разность между медианой и средней:
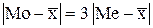 .
.
 2014-01-25
2014-01-25 1340
1340








