Тема 7. Ряды динамики

Индексный анализ динамики среднего уровня ряда (арифметического и гармонического индексов). Индексы качественных показателей (переменного, постоянного состава, структурных сдвигов).

Агрегатная форма индекса, элементы и принципы их построения. Веса в индексах. Агрегатные индексы качественных показателей. Индексный анализ относительного и абсолютного изменения объемного показателя.

В статистике исчисляются:

общий индекс физического объема услуг: 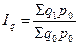(индекс Ласпейреса);

Он характеризует отношение объема услуг отчетного периода в базисных ценах к фактическому объему услуг в денежном выражении базисного периода. Разность между числителем и знаменателем индекса физического объема услуг отражает прирост объема услуг в денежном выражении за счет увеличения количества (физического объема) отдельных видов услуг: .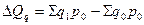

агрегатный индекс цен: I_p=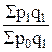(индекс Пааше);

Агрегатный индекс цен характеризует отношение стоимости услуг текущего периода к стоимости той же номенклатуры услуг, исчисленной в ценах базисного периода, и показывает, как в среднем изменилась цена услуг, произведенных в настоящее время.

Если бы цены на услуги снизились, то разность была бы отрицательной величиной и показывала экономию денежных средств (расходов) потребителей в результате снижения цен.

индекс стоимости продукции (услуг, товарооборота): I_qp .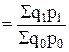

Он выражает изменение стоимости продукции (услуг, товарооборота), которое произошло за счет изменения как физического объема, так и цен.

Алгебраическая взаимосвязь рассматриваемых индексов выражается следующим образом. Индекс стоимости услуг равен произведению индекса физического объема услуг и индекса цен: .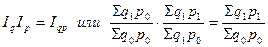

Все сказанное относительно индекса цен относится ко всем индексам качественных показателей.

Индекс себестоимости услуг: I_c=Sc₁q₁ / Sc₀q₁,

Индекс себестоимости услуг, рассчитанный по количеству услуг отчетного периода показывает, во сколько раз в среднем снизилась себестоимость услуг.

Разница между числителем и знаменателем индекса позволяет оценить реальную экономию затрат на производство услуг в результате снижения себестоимости услуг: ∆Э=Sc₁q₁ – Sc₀q₁.

Индекс производительности труда: I_t = St₀q₁ / St₁q₁.

Индекс производительноститруда оценивается на основе трудоемкости (t.), связанной с производительностью труда обратной зависимостью w=1/t. В качестве весов применяется также количество услуг отчетного периода: I_t = St₀q₁ / St₁q₁.

Разница между числителем и знаменателем индекса показывает реальную экономию трудовых затрат в результате роста производительности труда (снижения трудоемкости продукции): St₀q₁ – St₁q₁. Агрегатные индексы наиболее распространены.

Агрегатный индекс нельзя исчислить, если один из показателей задан в виде индивидуального индекса (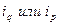). Тогда его заменяет средний индекс, тождественный агрегатному.

Индекс физического объема услуг может быть преобразован в средний арифметический индекс: I_q 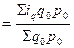; 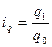, отсюда q₁ = i_q∙q₀.

Агрегатный индекс цен может быть преобразован в средний гармонический индекс: 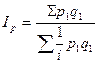. I_p = p₁/p₀, отсюда p₀ = p₁/i_р;

По формуле средней арифметической рассчитываются индекс физического объема продукции (услуг), производительности труда, по формуле средней гармонической индексы цен, себестоимости, трудоемкости и материалоемкости продукции.

Средние индексы широко используются для анализа рынка ценных бумаг. Индекс Доу-Джонса рассчитывается как средний арифметический индекс значений курсов акций, котирующихся на фондовой бирже.

Для изучения динамики экономических явлений за несколько периодов используется система цепных и базисных индексов. Если индексируемые величины сравниваются с уровнем одного и того же периода, то говорят о системе базисных индексов. При оценке относительного изменения уровня изучаемого явления по сравнению с предшествующим периодом получают систему цепных индексов.

Влияние отдельных факторов на совокупное изменение результативного показателя оценивается с помощью индексного метода, основанного на построении системы взаимосвязанных индексов. Индексный метод факторного анализа может применяться только в тех случаях, когда между результативными и факторными показателями имеется функциональная связь. Система взаимосвязанных индексов должна выразить индекс результативного показателя в виде математической зависимости индексов факторных показателей. Например, взаимосвязаны между собой объем услуг (доходы) предприятия, производительность труда и численность работников (Q = WT); затраты на производство, себестоимость и объем услуг (Э = cQ); фонд заработной платы, средняя заработная плата и численность работников (З = зТ). Если взять отношения каждой из этих зависимостей за два периода, то получатся аналогичные выражения для взаимосвязанных индексов: I_Q = I_WI_T; I_Э = I_cI_Q; I_З = I_зI_Т.

По аналогии с рассмотренными взаимосвязанными индексами стоимости продукции (услуг, товарооборота), физического объема продукции (услуг) и цен строятся следующие сводные индексы:

издержек производства, физического объема продукции (услуг) и себестоимости продукции (услуг) I_qc = I_q∙I_c

; ; ,

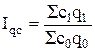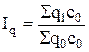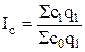где с₀, с₁ – себестоимость продукции (услуг) в базисном, отчетном периодах;

затрат времени на производство продукции (услуг), физического объема продукции (услуг) и производительности труда по трудовым затратам I_qt = I_q∙I_t

; ; ,

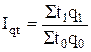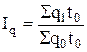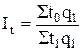где t₀, t₁ – затраты рабочего времени на производство услуг в базисном, отчетном периодах.

Такие системы привлекаются для расчетов одного из показателей, входящих в систему, если известны два других. Например, известно, что себестоимость услуг предприятия снизилась на 6%, объем услуг в денежном выражении увеличился на 15%. Зная, что динамика затрат на производство I_Э определяется произведением индексов себестоимости услуг I_с и объема услуг I_Q, можно легко узнать, как изменятся издержки производства в данном предприятии: I_Э=I_cI_Q=0,94×1,15=1,082, т.е. они увеличатся на 8,2%.

Все рассмотренные выше индексы рассчитываются при условии, что качественные показатели и их веса не учитывали структуру предприятия (цеха, филиалы, категории потребителей)

Однако динамика изучаемых социально-экономических явлений и процессов также обусловлена структурными сдвигами. Данная задача решается с помощью построения системы взаимосвязанных индексов переменного состава, постоянного состава и влияния структурных сдвигов. В этой системе динамика среднего показателя (индекс переменного состава) представляет собой произведение двух индексов: индекса среднего показателя в неизменной структуре (индекса постоянного состава) и индекса среднего показателя, отражающего изменения структуры совокупности (индекса структурных сдвигов): I_пер = I_пост I _стр.

Индекс переменного состава среднего показателя вычисляется как отношение двух средних арифметических взвешенных величин, относящихся к отчетному и базисному периодам, и отражает влияние двух факторов: изменения индексируемой величины в неизменной структуре (с постоянными весами) и изменения индексируемой величины в результате структурных сдвигов (с переменными весами). Чтобы выявить раздельное влияние этих факторов на динамику среднего показателя, произведем следующее преобразование в условных обозначениях, принятых для средней:

I_x ,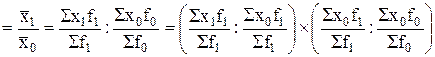

где х₁, х₀ – групповые средние в отчетном и базисном периодах; f₁, f₀ – численность единиц совокупности или вес каждой группы в отчетном и базисном периодах.

В данной схеме первое соотношение представляет собой индекс переменного состава I_пер, второе – индекс постоянного состава I_пост, третье – индекс структурных сдвигов I_стр. Эта общая схема построения системы взаимосвязанных индексов переменного, постоянного состава и структурных сдвигов. При этом следует отметить, что индекс постоянного состава представляет собой агрегатный индекс:

I_пост .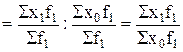

Для практических расчетов индекса структурных сдвигов используют следующую формулу: I_стр .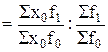

Влияние каждого фактора на результативный показатель (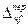) в абсолютном выражении определяется разностью числителя и знаменателя, умноженной на весовой показатель в последующем периоде :

; ; .

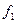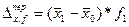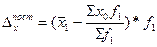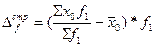Система взаимосвязанных индексов переменного, постоянного состава и структурных сдвигов может участвовать в анализе реализации плана средних уровней качественных показателей: себестоимости услуг, фондоемкости услуг, производительности труда, фондоотдачи, средней заработной платы и др.

Для анализа динамики производительности труда используются следующие формулы для расчета индексов переменного состава, постоянного состава и влияния структурных сдвигов:

общее изменение средней производительности труда: ;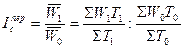

изменение средней производительности труда за счет изменения производительности труда в структурных единицах: ;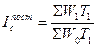

изменение средней производительности труда за счет изменения численности работников в структурных единицах: .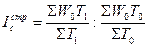

Поскольку объем услуг (доходы) предприятия, производительность труда и численность работников взаимосвязаны между собой (Q = WT), то влияние каждого фактора на результативный показатель (Q) в абсолютном выражении определяется разностью числителя и знаменателя, умноженной на численность работников в последующем периоде :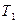

; ; .

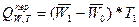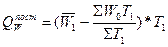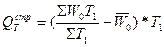Экономический эффект в случае роста средней производительности труда заключается кроме увеличения величины доходов в условной экономии численности работников: .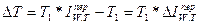

7.1 Понятие и классификация рядов динамики: основные элементы и виды динамических рядов. Сопоставимость рядов динамики, смыкание рядов динамики.

Статистическая наука, руководствуясь принципами диалектического метода познания, разрабатывает основные правила и приемы анализа рядов динамики, характеристики тенденций и темпов развития социально-экономических явлений, числового оценивания происходящих в них изменений.

Ряды динамики представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Составными элементами ряда динамики являются показатели уровней ряда «y», и показатели времени: периоды (годы, кварталы, месяцы, сутки) или моменты (даты) «t».

В зависимости от способа выражения уровней ряды динамики делятся на ряды абсолютных, относительных и средних величин.

Например, ряды динамики средних величин образует динамика среднегодовой производительности труда работников за ряд лет, ряды динамики относительных величин образует изменение доли доходов документальной связи в общей сумме доходов организаций электросвязи за несколько периодов.

Разновидностями рядов динамики относительных и средних величин являются ряды темпов роста, изменения структуры совокупности, изменения показателей интенсивности (телефонной плотности, радиуса обслуживания).

Вид ряда динамики обусловливается сущностью, внутренним содержанием изучаемого явления. Размеры одних явлений фиксируются на какую-либо дату, момент времени (количество телефонных станций, телевизионных передатчиков, пунктов связи, численность работников, стоимость активов), размеры других явлений устанавливаются при рассмотрении их в течение какого-либо промежутка времени (объем услуг, выручка от реализации услуг, затраты на производство услуг).