В зависимости от способа выражения периода времени, за который характеризуется развитие явления, ряды динамики делятся на два вида: моментные(наопределенную дату) и интервальные (за определенные интервалы времени – сутки, месяц, квартал).
Понятия уровней интервального и моментного рядов различаются: объем услуг, доходов связи, затрат на производство услуг связи – накопленный итог деятельности за какой-либо период; численность работников, количество каналов, стоимость основных фондов представляют собой среднюю величину, изменяющуюся со временем в результате баланса (увеличения и уменьшения).
Сущность явлений в рядах различных видов обусловливает важное правило: показатели интервальных рядов можно складывать, показатели моментных рядов не обладают свойством суммирования. Например, если сложить данные о ежедневном объеме услуг (трафика) и получится месячный итог; сложив месячные итоги, получим объем услуг (трафика) за год.
В зависимости от расстояния между уровнями ряды динамики подразделяются на ряды динамики с равноотстоящими уровнями (следующими друг за другом периодами) и не равноотстоящими уровнями (с прерывающимися периодами).
Анализ охватывает, как правило, большой период времени, в течение которого могли произойти всевозможные изменения. Для того, чтобы анализ ряда был объективным, все уровни ряда должны быть сопоставимы.
Несопоставимость статистических данных объясняется различными причинами, например, изменение цен, тарифов на услуги связи, появление новых услуг связи, изменение территориальных границ, единиц измерения или счета, различия в методологии учета и расчета показателей, по организации статистических наблюдений объектов, различия в методологии подсчета статистических показателей разных стран.
Одним из способов приведения данных в сопоставимый вид является смыкание рядов динамики или приведения к одному основанию.
Под смыканием рядов динамики понимают объединение в один ряд (более длинный) двух или нескольких рядов, уровни которых исчислены по разной методологии или разным территориальным границам. При этом важно, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методике или в разных границах.
При параллельном анализе развития во времени социально-экономических показателей отдельных административных и территориальных единиц, регионов и стран в целях обеспечения сопоставимости ряды динамики приводят к одному основанию, т.е. периоду времени (или моменту времени), уровень которого принимается за базу сравнения. Остальные уровни выражаются в процентах или в виде коэффициентов по отношению к нему.
При изучении рядов динамики для анализа скорости и интенсивности развития явления во времени исчисляют следующие показатели: средний уровень, темп роста и прироста, абсолютный прирост, абсолютное значение одного процента прироста, средний темп роста.
Анализ рядов динамики начинается с определения среднего уровня явления за те или иные промежутки времени. Средний уровень дает общую характеристику показателя за весь период, охватываемый рядом динамики. Средний уровень в интервальном и моментном рядах динамики определяется по-разному.
В интервальном динамическом ряду с равными интервалами средний уровень рассчитывается по формуле простой средней арифметической 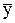 = Syi/n.
= Syi/n.
В моментном ряду динамики средний уровень определяется по формуле средней хронологической:
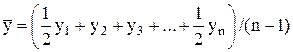 ,
,
где n – число уровней ряда динамики; y1, y2,..., yn – первый, второй,..., n-й члены моментного ряда динамики.
По приведенной формуле средний уровень может быть исчислен только для такого ряда, в котором все члены равно отстоят друг от друга, например, если все данные приведены на начало каждого месяца, квартала или года.
В случае неравных интервалов времени между моментами (фактами) средний уровень определяется по средней арифметической взвешенной, в качестве весов в которой принимается время между значениями моментов 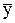 = Syt/St, где t – количество дней (месяцев, лет), в течение которых сохранялось данное значение уровня ряда.
= Syt/St, где t – количество дней (месяцев, лет), в течение которых сохранялось данное значение уровня ряда.
Характеристику интенсивности и относительной скорости изменения уровней ряда динамики получают на основе расчета темпов роста и прироста (абсолютного и относительного).
Темпы – это относительные величины, характеризующие направление и интенсивность развития.
Темп роста представляет собой отношение одного уровня ряда к другому и показывает, во сколько раз один уровень больше другого. Если все уровни ряда сопоставить с уровнем одного какого-либо периода, принятого за базу сравнения (обычно начального), то получается ряд базисных темпов роста, если сопоставление производится по отношению к уровню предыдущего периода, то образуется ряд цепных темпов роста:
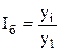 ;
; 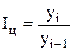 ,
,
где yi уровень i-го члена ряда; yi-1 – уровень предшествующего i-му члена ряда; y1 – уровень начального (базисного) члена ряда.
Темпы роста выражаются либо в коэффициентах, если основание сравнения принимается за единицу, либо в процентах, если основание сравнения принимается за 100.
Базисные темпы роста дают характеристику непрерывного развития и показывают для каждого года изменение количества по сравнению с годом, принятым за базу.
Цепные темпы роста характеризуют интенсивность развития в каждом отдельном периоде, в данном примере – за каждый год.
Между базисными и цепными темпами роста существует взаимосвязь: произведение цепных темпов равно базисному, частное от деления базисных темпов равно промежуточному цепному темпу.
Эти соотношения можно выявить, если записать индексы в буквенных обозначениях. Представим произведение трех цепных индексов:
I2/1I3/2I4/3 = 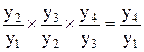 = I4/1.
= I4/1.
Из записи видно, что промежуточные уровни сокращаются и в результате получается отношение конечного уровня к начальному, т.е. базисный темп роста.
Теперь разделим два базисных темпа роста, например, за четвертый и третий периоды:
I4/1: I3/1 = 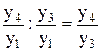 = I4/3.
= I4/3.
Получен цепной темп роста.
Во всех расчетах, когда проводятся математические преобразования одних темпов роста в другие, темпы роста следует выражать в коэффициентах, а не в процентах.
Чтобы установить, насколько изменился уровень явления в одном периоде по сравнению с другим, используют показатели абсолютного прироста и темпов прироста.
Абсолютный прирост исчисляется как разность уровней ряда динамики и выражается в тех же единицах измерения, что и показатели ряда. Можно исчислять приросты за каждый период в отдельности: yi–yi–1 (например, ежегодные приросты), и с начала исследуемого периода: yi–y1 (накопленные приросты). Накопленный прирост равен сумме приростов (снижений) за отдельные периоды.
Оценку абсолютного прироста дают относительные показатели темпа прироста. Темпы прироста делятся на цепные и базисные и исчисляются делением абсолютного прироста на предыдущий (или первоначальный) уровень и выражаются в процентах. Цепные приросты: 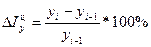 , базисные приросты:
, базисные приросты: 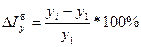 .
.
Темп прироста характеризует относительную скорость изменения уровня ряда в единицу времени и показывает, на сколько процентов увеличились или уменьшились размеры явления за изучаемый период. Темп прироста можно получить непосредственно из темпа роста. Для этого следует из темпа роста, выраженного в процентах, вычесть 100; DI=I–100 %.
Абсолютное значение одного процента прироста равно частному от деления абсолютного прироста на темп прироста в процентах:
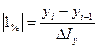 .
.
Чтобы охарактеризовать интенсивность развития явления за длительный период, определяют средний (обычно среднегодовой) темп роста как среднюю величину из ежегодных темпов роста. Среднегодовой темп роста служит сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики и показывает во сколько раз в среднем за единицу времени (за год) изменился уровень динамического ряда.
 2014-01-25
2014-01-25 1089
1089
