Агрегатная форма является исходной формой выражения сводного индекса. При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы. Цены различных товаров, реализуемых в розничной торговле, складывать неправомерно, однако, с экономической точки зрения, вполне допустимо суммировать товарооборот по этим товарам. Если мы сравним товарооборот по n видам товаров в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:
I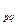 =
=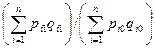
Где pi1 и pi0 –цена, а qi1 и qi0 – объем продаж i-го товара соответственно в текущем и базисном периодах.
Числитель данного индекса представляет собой товарооборот текущего периода (сумма цен различных товаров, умноженных на объемы их реализации), знаменатель- товарооборот предшествующего периода.
На величину индекса товарооборота оказывают влияние как изменение цен на товары, так и изменение объемов их реализации. Для того, что бы оценить изменение только цен необходимо кол-во проданных товаров (веса индексов) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей как цена, себестоимость, производительность труда, урожайность количественный показатель обычно фиксируют на уровне текущего периода. Таким образом получают сводный индекс цен (Пааше):
I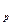 =
=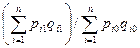
Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих 2х категорий и отражает имевшее место изменение цен.
Индекс цен Пааше показывает, насколько товары в текущем периоде подорожали (подешевели) по сравнению с базисным периодом, а индекс цен Ласпейерса показывает, во ск-ко раз товары базисного периода дороже (дешевле) в результате изменений цен в отчетном периоде. Как правило, индекс цен, рассчитанный по формуле Паше, несколько занижает, а по формуле Ласпейерса- завышает темпы инфляции.
Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. он характеризует изменение кол-ва проданных товаров не в денежных, а в физических единицах измерения:
I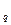 =
=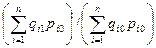
Весами в данном индексе выступают цены, которые фиксируются на базисном уровне. Между рассчитанными индексами также существует взаимосвязь:
IpIq=Ipq
Рассмотрим применение индексного метода при анализе изменения затрат на производство и себестоимость продукции. Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода:
I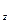 =
=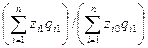

Где zi1 и zi0 –себестоимость i-Го вида продукции соответственно в текущем и базисном периодах.
Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель- условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии или потерь предприятия от изменения себестоимости:
E=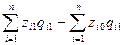
Сводный индекс физического объема продукции, взвешенный по себестоимости, имеет след. Вид:
I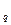 =
=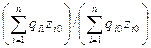
Третьим показателем в данной индексной системе явл-ся сводный индекс затрат на производство:
I 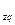 =
=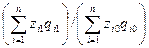
Все три индекса взаимосвязаны между собой соотношением:
IzIq=Izq
Еще одна область применения индексного метода- анализ изменений в производительности труда. При этом возможны 2 подхода к расчету индексов. Первый основан на учете количества продукции, вырабатываемого в единицу времени (w). При таких расчетах необходимо решить ряд методологических проблем- какой именно показатель продукции использовать, как оценивать продукцию работников непроизводственных отраслей и пр.
При втором подходе производительность труда определяется затратами рабочего времени на единицу продукции (t).На практике эти расчеты также сопряжены с определенными трудностями, так как не всегда имеется возможность оценить вклад конкретного работника в производство того или иного изделия.
Количество продукции w, вырабатываемое в единицу времени (в натур. Выражении), и затраты времени t на единицу продукции взаимосвязаны между собой:
W=
Индивидуальные индексы производительности труда, основанные на этих показателях, имеют след. Вид:
i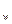 =
= 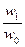 =
=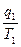 :
: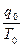
i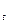 =
= 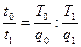
Где T- суммарные затраты времени на выпуск данной продукции в чел.-ч., чел.-днях или чел.-мес. (в последнем случае соответствует общей численности работников).
Располагая данными о трудоемкости n различных видов продукции (i=1,2,…, п) и объем их производства, можно рассчитать сводный индекс производительности труда (по трудоемкости):
I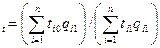
Знаменатель этого индекс отражает реально имевшие место затраты времени на выпуск всей продукции в текущем периоде (T) Числитель представляет собой условную величину, показывающую, если бы трудоемкость не изменилась.
При расчете сводного индекса производительности труда в стоимостном выражении (по выработке) необходимо количество продукции, произведенной за каждый период, взвесить по каким-либо ценам, принятым за сопоставимые. В качестве сопоставимых могут выступать цены текущего или базисного периода, какого-либо др периода или средние цены. Индекс в этом варианте рассчитывается по формуле:
I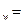 (
(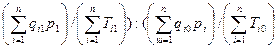 )
)
Первая часть этой формулы представляет собой среднюю выработку в отчетном периоде, вторая часть –в базисном.
Умножение индекса производительности труда по выработке на индекс затрат рабочего времени дает индекс физического объема продукции, взвешенный по цене:
I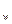 I
I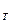 = I
= I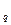 или
или 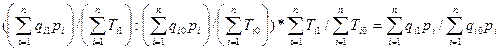
Cводные индексы в среднегармонической и среднеарифметической формах.
В ряде случаев вместо индексов в агрегатной форме удобнее использовать арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней нужно выбрать таким образом, что бы полученный средний индекс был тождественен исходному агрегатному индексу.
Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде (p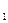 q
q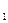 ) и индивидуальными индексами цен (i
) и индивидуальными индексами цен (i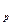 =
=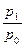 ), полученными, скажем, в результате выборочного наблюдения. Тогда в знаменателе сводного индекса цен
), полученными, скажем, в результате выборочного наблюдения. Тогда в знаменателе сводного индекса цен
(I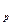 = (
= (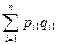 ) / (
) / (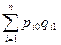 ))
))
Можно использовать следующую замену:
p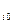 =
= 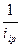 p
p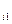
Таким образом, сводный индекс цен будет выражен как средний гармонический индекс:
I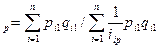
При расчете сводного индекса физического объема товарооборота можно использовать среднеарифметическую форму.
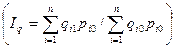
При этом в числителе производится замена:
qi1=iiqqi0
Тогда индекс примет вид:
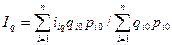
В среднеарифметической форме также может рассчитываться и индекс производительности труда по трудоемкости, известный как индекс С.Г. Струмилина:
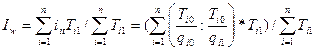
 2014-01-25
2014-01-25 853
853








