Скалярным произведением векторов 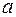 и
и 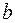 называют число, равное произведению модулей перемножаемых векторов на косинус угла
называют число, равное произведению модулей перемножаемых векторов на косинус угла 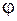 между ними.
между ними.
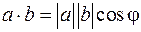 .
.
Скалярное произведение двух векторов является числом (скаляром).
Свойства скалярного произведения
1. Скалярное произведение двух векторов обращается в нуль, если вектора взаимно перпендикулярны или если один сомножитель (или оба) есть нуль-векторы (то есть 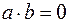 , если
, если 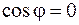 , или если
, или если 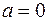 или
или 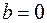 или
или 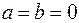 ).
).
2. Скалярный «квадрат» вектора равен квадрату его длины: 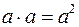 (так как при
(так как при 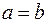 угол
угол 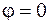 и
и 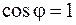 ).
).
3. Скалярное произведение не изменяет своего значения при перестановке сомножителей (свойство коммутативности) 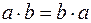 (так как
(так как 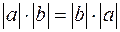 и
и 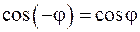 ).
).
4. Скалярное произведение равно произведению длины одного из перемножаемых векторов на проекцию другого вектора на направление первого; 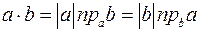 , то есть
, то есть 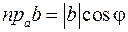 ;
; 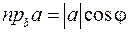 .
.
5. Скалярное произведение обладает распределительным свойством 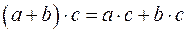 .
.
6. Чтобы умножить скалярное произведение на числовой множитель, достаточно на этот множитель умножить один из перемножаемых векторов: 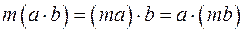 .
.
 2014-01-25
2014-01-25 723
723








