через координаты перемножаемых векторов
Пусть даны векторы: 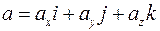 и
и 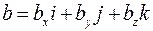 .
.
Тогда, 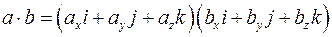 .
.
В силу 5 и 6 можно представить это как произведение многочлена на многочлен:
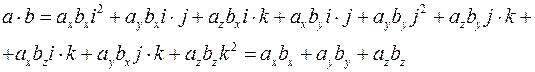
Все произведения, кроме скалярных квадратов, равны нулю, так как входящие в них векторы ортогональны.
Итак, скалярное произведение равно сумме попарных произведений одноименных проекций векторов, так как 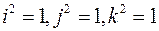 .
.
Условие перпендикулярности векторов может быть таким:
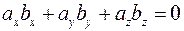 .
.
Скалярным произведением двух векторов можно воспользоваться для вычисления угла между ними:
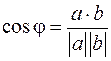 или
или 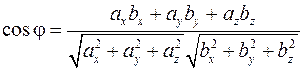 .
.
Отсюда и находим условие перпендикулярности (ортогональности) двух векторов: 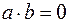 или
или 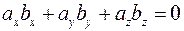 .
.
 2014-01-25
2014-01-25 703
703








