Свойства векторного произведения

1. Векторное произведение двух векторов равно нулю, если один или оба сомножителя являются нуль-векторам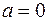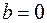и (, или 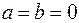), или же, если сомножители являются коллинеарными векторам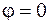и (или 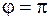), в частности .

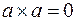2. При перестановке местами векторов-сомножителей векторное произведение изменяет знак, то есть превращается в противоположный вектор:

.

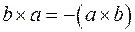3. Векторное произведение не обладает коммутативностью. В самом деле .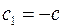

4. Векторное произведение векторов обладает распределительным свойством:

.

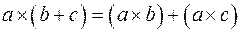5. Чтобы умножить векторное произведение двух векторов на произвольный числовой множитель, достаточно умножить на него один из перемножаемых векторов (любой ): .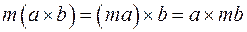

Вычисление векторного произведения через проекции

(координаты) перемножаемых векторов

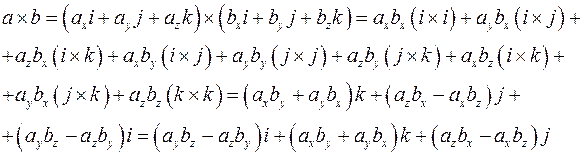
и это, как нетрудно убедиться, определитель

.

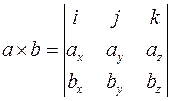Замечание: При помощи векторного произведения легко вычислить площадь треугольника, стороны которого заданы векторами или вершины – их координатами.

Пример: найти площадь треугольника, вершинами которого служат точк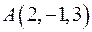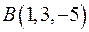и , и .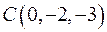

Решение: находим векторы , ;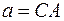

,

.

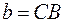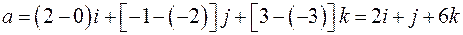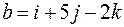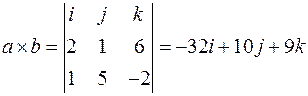
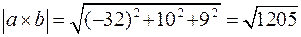
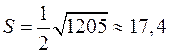(ед²).