Прямые в пространстве

Решение.

По формуле (11) получаем .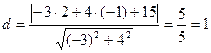

Лекция 3

Контрольные вопросы:

1. Уравнение прямой в пространстве, проходящей через две заданные точки.

2. Уравнение прямой в пространстве, заданной как линия пересечения плоскостей.

3. Канонические уравнения прямой в пространстве.

4. Параметрические уравнения прямой в пространстве.

5. Угол между двумя прямыми.

6. Условие компланарности двух прямых.

7. Угол между прямой и плоскостью.

8. Условия параллельности и перпендикулярности прямой и плоскости.

1. Уравнения прямой в пространстве, проходящей через две заданные точки 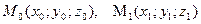, имеют вид

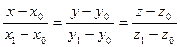. (1)

2. Прямая может быть задана уравнениями двух плоскостей

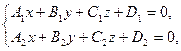
пересекающихся по этой прямой.

3. Канонические уравнения прямой

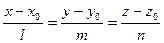
определяют прямую, проходящую через точку 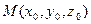параллельно вектору .

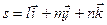4. Параметрические уравнения прямой

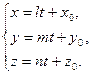
5. Угол между двумя прямыми, заданными их каноническими уравнениям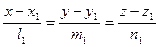и и 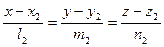, определяется по формуле

.

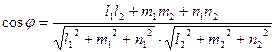6. Необходимое и достаточное условие нахождения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):

.

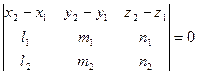Если величины 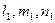не пропорциональны величинам 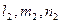, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.

7. Угол между прямой 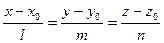и плоскостью 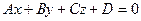определяется по формуле

;

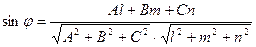условие параллельности прямой и плоскости:

;

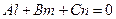условие перпендикулярности прямой и плоскости:

.

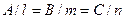Пример 1. Составить уравнение прямой, проходящей через точки А₁(4; -3; 1), А₂(5; -3; 0).