Найдем нормирующий множитель 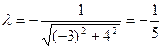 .
.
Умножая данное уравнение на λ, получим искомое нормальное уравнение прямой: 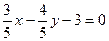 .
.
10. Угол между прямыми. Если прямые 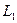 и
и 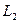 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 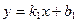 и
и 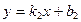 соответственно, то тангенс угла между этими прямыми можно вычислить по формуле
соответственно, то тангенс угла между этими прямыми можно вычислить по формуле
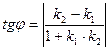 . (10)
. (10)
11. Условие параллельности двух прямых. Для того чтобы прямые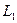 и
и 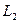 , заданные уравнениями с угловыми коэффициентами
, заданные уравнениями с угловыми коэффициентами 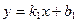 и
и 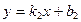 соответственно, были параллельны, необходимо и достаточно, чтобы
соответственно, были параллельны, необходимо и достаточно, чтобы 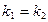 .
.
Для того чтобы прямые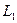 и
и 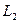 , заданные уравнениями
, заданные уравнениями 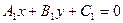 и
и 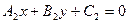 соответственно, были параллельны, необходимо и достаточно, чтобы
соответственно, были параллельны, необходимо и достаточно, чтобы 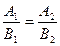 .
.
12. Условие перпендикулярности двух прямых. Для того чтобы прямые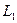 и
и 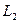 , заданные уравнениями с угловыми коэффициентами
, заданные уравнениями с угловыми коэффициентами 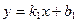 и
и 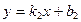 соответственно, были перпендикулярны, необходимо и достаточно, чтобы
соответственно, были перпендикулярны, необходимо и достаточно, чтобы 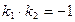 .
.
Для того чтобы прямые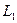 и
и 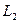 , заданные уравнениями
, заданные уравнениями 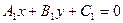 и
и 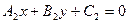 соответственно, были перпендикулярны, необходимо и достаточно, чтобы
соответственно, были перпендикулярны, необходимо и достаточно, чтобы 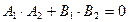 .
.
13. Расстояние от точки до прямой. Если прямая 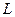 задана уравнением
задана уравнением 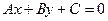 и точка
и точка 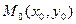 не принадлежит данной прямой, то расстояние от точки до прямой находится по формуле
не принадлежит данной прямой, то расстояние от точки до прямой находится по формуле
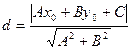 . (11)
. (11)
Пример 2. Найти расстояние от точки 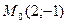 до прямой
до прямой 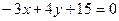 .
.
 2014-01-25
2014-01-25 759
759








