Решение.
По формуле 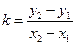 найдем угловой коэффициент стороны АВ; имеем
найдем угловой коэффициент стороны АВ; имеем 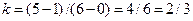 . В силу условия перпендикулярности угловой коэффициент высоты, проведенной их вершины С, равен -3/2. уравнение этой высоты имеет вид
. В силу условия перпендикулярности угловой коэффициент высоты, проведенной их вершины С, равен -3/2. уравнение этой высоты имеет вид 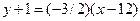 , или
, или 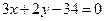 .
.
Лекция 2
Контрольные вопросы:
1. Общее уравнение прямой.
2. Уравнение прямой с угловым коэффициентом.
3. Уравнение прямой в отрезках.
4. Уравнение прямой, проходящей через данную точку в данном направлении.
5. Уравнение пучка прямых.
6. Уравнение прямой, проходящей через две точки.
7. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
8. Полярное уравнение прямой.
9. Нормальное уравнение прямой.
10. Угол между прямыми.
11. Условие параллельности двух прямых.
12. Условие перпендикулярности двух прямых.
13. Расстояние от точки до прямой.
1. Общее уравнение прямой. Всякое уравнение первой степени с двумя неизвестными х и у, т.е. уравнение вида
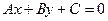 (1)
(1)
(где А, В, С – постоянные коэффициенты, причем 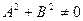 ) определяет на плоскости прямую. Это уравнение называется общим уравнением прямой.
) определяет на плоскости прямую. Это уравнение называется общим уравнением прямой.
Частные случаи общего уравнения прямой:
1) если 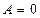 , то уравнение приводится к виду
, то уравнение приводится к виду 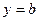 , где
, где 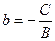 (это есть уравнение прямой, параллельной оси Ох);
(это есть уравнение прямой, параллельной оси Ох);
2) если 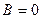 , то уравнение прямой приводится к виду
, то уравнение прямой приводится к виду 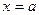 , где
, где 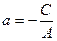 (прямая параллельна оси Оу);
(прямая параллельна оси Оу);
3) если 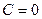 , то уравнение приводится к виду
, то уравнение приводится к виду 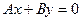 (прямая проходит через начало координат).
(прямая проходит через начало координат).
2. Уравнение прямой с угловым коэффициентом. Если в общем уравнении прямой 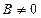 , то, разрешив его относительно у, получим уравнение вида
, то, разрешив его относительно у, получим уравнение вида
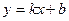 , (2)
, (2)
где 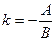 ,
, 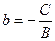 . Его называют уравнением прямой с угловым коэффициентом.
. Его называют уравнением прямой с угловым коэффициентом.
3. Уравнение прямой в отрезках. Если в общем уравнении прямой 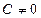 , то, разделив все его части на (– С), получим уравнение вида
, то, разделив все его части на (– С), получим уравнение вида
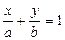 , (3)
, (3)
где 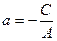 ,
, 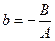 .
.
4. Уравнение прямой, проходящей через данную точку в данном направлении. Если прямая проходит через точку 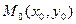 и ее направление характеризуется угловым коэффициентом k, то уравнение прямой имеет вид
и ее направление характеризуется угловым коэффициентом k, то уравнение прямой имеет вид
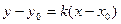 . (4)
. (4)
5. Данное уравнение (4) с различными значениями коэффициента k называют также уравнениями пучка прямых с центром в точке 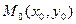 .
.
6. Уравнение прямой, проходящей через две точки. Если прямая проходит через точки 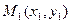 и
и 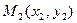 , то уравнение прямой имеет вид
, то уравнение прямой имеет вид
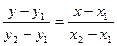 , (5)
, (5)
где 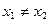 ,
, 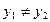 .
.
7. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Если прямая проходит через заданную точку 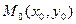 перпендикулярно данному ненулевому вектору
перпендикулярно данному ненулевому вектору 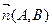 , то уравнение прямой имеет вид
, то уравнение прямой имеет вид
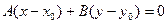 . (6)
. (6)
Вектор 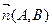 , перпендикулярный прямой, называется нормальным вектором этой прямой.
, перпендикулярный прямой, называется нормальным вектором этой прямой.
8. Полярное уравнение прямой. Положение прямой в полярных координатах определено, если указано расстояние р. от полюса О до данной прямой и угол α между полярной осью ОР и осью l, проходящей через полюс О перпендикулярно данной прямой (рис.1).

Рис.1
Для любой точки 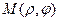 на данной прямой имеем
на данной прямой имеем
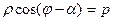 . (7)
. (7)
Прямоугольные координаты (х; у) точки М и ее полярные координаты 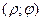 связаны соотношениями:
связаны соотношениями:
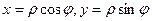 (*)
(*)
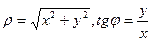 (**)
(**)
где 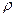 - полярный радиус,
- полярный радиус, 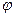 - полярный угол точки М (рис. 2).
- полярный угол точки М (рис. 2).
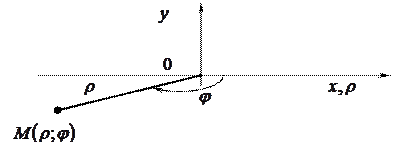
Рис.2
9. Нормальное уравнение прямой. Если прямая определяется заданием p и α (рис. 3), то уравнение (7) прямой в прямоугольной системе координат имеет вид
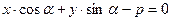 . (8)
. (8)
Уравнение (8) можно получить из общего уравнения прямой (1), умножив обе части данного уравнения на нормирующий множитель
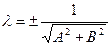 , (9)
, (9)
учитывая, что знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.

Рис.3
Пример 1. Привести уравнение 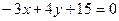 к нормальному виду.
к нормальному виду.
 2014-01-25
2014-01-25 716
716








