Промежуточные расчеты параметров линейной модели по формулам (3.5 ) приведены в табл. 4.3.15.
Табл. 4.3.15
| № | 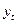
| 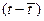
| 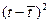
| 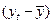
| 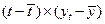
| 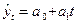
|  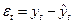
|
| -5,5 | 30,25 | -5 | 27,5 | 40,04 | 4,96 | ||
| -4,5 | 20,25 | -10 | 41,85 | -1,85 | |||
| -3,5 | 12,25 | -7 | 24,5 | 43,66 | -0,66 | ||
| -2,5 | 6,25 | -2 | 45,47 | 2,53 | |||
| -1,5 | 2,25 | -8 | 47,28 | -5,28 | |||
| -0,5 | 0,25 | -3 | 1,5 | 49,09 | -2,09 | ||
| 0,5 | 0,25 | 0,5 | 50,91 | 0,09 | |||
| 1,5 | 2,25 | 7,5 | 52,72 | 2,28 | |||
| 2,5 | 6,25 | 54,53 | -4,53 | ||||
| 3,5 | 12,25 | 24,5 | 56,34 | 0,66 | |||
| 4,5 | 20,25 | 58,15 | 1,85 | ||||
| 5,5 | 30,25 | 59,96 | 2,04 | ||||
| 6,5 |
При вычислении «вручную» по формуле (3.4) получаем те же результаты:
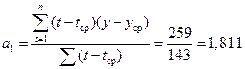 ,
,
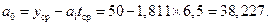
Табл. 4.3.16.
| A | B | C | D | E | F | G | H | |
| ВЫЧИСЛЕНИЯ В EXCEL С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ | ||||||||
| № | 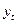
| 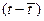
| 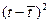
| 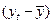
| 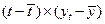
| 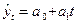
| 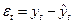
| |
| =B2-$J$15 | =D2*D2 | =C2-$K$15 | =D2*F2 | =$M$21+$M$18*B2 | =C2-H2 | |||
| =B3-$J$15 | =D3*D3 | =C3-$K$15 | =D3*F3 | =$M$21+$M$18*B3 | =C3-H3 | |||
| =B4-$J$15 | =D4*D4 | =C4-$K$15 | =D4*F4 | =$M$21+$M$18*B4 | =C4-H4 | |||
| =B5-$J$15 | =D5*D5 | =C5-$K$15 | =D5*F5 | =$M$21+$M$18*B5 | =C5-H5 | |||
| =B6-$J$15 | =D6*D6 | =C6-$K$15 | =D6*F6 | =$M$21+$M$18*B6 | =C6-H6 | |||
| =B7-$J$15 | =D7*D7 | =C7-$K$15 | =D7*F7 | =$M$21+$M$18*B7 | =C7-H7 | |||
| =B8-$J$15 | =D8*D8 | =C8-$K$15 | =D8*F8 | =$M$21+$M$18*B8 | =C8-H8 | |||
| =B9-$J$15 | =D9*D9 | =C9-$K$15 | =D9*F9 | =$M$21+$M$18*B9 | =C9-H9 | |||
| =B10-$J$15 | =D10*D10 | =C10-$K$15 | =D10*F10 | =$M$21+$M$18*B10 | =C10-H10 | |||
| =B11-$J$15 | =D11*D11 | =C11-$K$15 | =D11*F11 | =$M$21+$M$18*B11 | =C11-H11 | |||
| =B12-$J$15 | =D12*D12 | =C12-$K$15 | =D12*F12 | =$M$21+$M$18*B12 | =C12-H12 | |||
| =B13-$J$15 | =D13*D13 | =C13-$K$15 | =D13*F13 | =$M$21+$M$18*B13 | =C13-H13 | |||
| =СРЗНАЧ (A2:A13) | =СРЗНАЧ (B2:B13) | =СУММ (D2:D13) | =СУММ (F2:F13) | =СУММ (H2:H13) | ||||
| a1= | =G14/E14 | |||||||
| a0= | =C14-E17*B14 | |||||||
2) оценка качества построенной модели.
2.1) Оценка адекватности
Для оценки адекватности построенных моделей исследуются свойства остаточной компоненты, т.е. расхождения уровней, рассчитанных по модели, и фактических наблюдений (табл. 4.3.17).
Табл. 4.3.17.
| № | 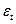
| Точки поворота | 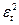
| 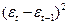
|
| 4,962 | 24,617 | |||
| -1,850 | * | 3,421 | 46,392 | |
| -0,661 | 0,437 | 1,413 | ||
| 2,528 | * | 6,391 | 10,169 | |
| -5,283 | * | 27,912 | 61,015 | |
| -2,094 | 4,387 | 10,169 | ||
| 0,094 | 0,009 | 4,791 | ||
| 2,283 | * | 5,213 | 4,791 | |
| -4,528 | * | 20,503 | 46,392 | |
| 0,661 | 0,437 | 26,924 | ||
| 1,850 | 3,421 | 1,413 | ||
| 2,038 | 4,155 | 0,036 | ||
| 100,902 | 213,504 |
· При проверке независимости (отсутствие автокорреляции) определяется отсутствие в ряду остатков систематической составляющей, например, с помощью d-критерия Дарбина–Уотсона по формуле (3.7):
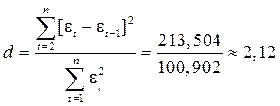
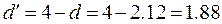
Так как 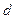 попало в интервал от d 2, до 2 то по данному критерию можно сделать вывод о выполнении свойства независимости.
попало в интервал от d 2, до 2 то по данному критерию можно сделать вывод о выполнении свойства независимости.
Это означает, что в ряду динамики не имеется автокорреляции, следовательно, модель по этому критерию адекватна.
· Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек (формула (3.6)). Количество поворотных точек (p) равно 5 (рис. 3.4.14).
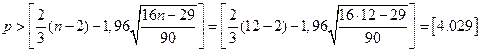
Неравенство выполняется (5>4). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.
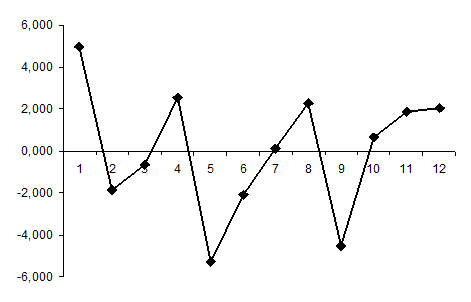
Рис. 3.4.14. График остатков
· Соответствие ряда остатков нормальному закону распределения определим при помощи RS-критерия:
RS= [ 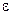 max –
max –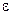 min] /
min] / 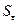 ;
;
где 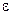 max – максимальный уровень ряда остатков,
max – максимальный уровень ряда остатков, 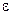 max = 4 ,9 62;
max = 4 ,9 62;
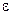 min – минимальный уровень ряда остатков,
min – минимальный уровень ряда остатков, 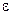 min = – 4,528;
min = – 4,528;
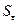 – среднеквадратическое отклонение,
– среднеквадратическое отклонение,
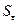 =
=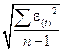 =
= 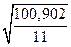 = 3,029;
= 3,029;
RS =[4 ,9 62 – (– 5.28 3)] / 3,029 = 3,383
Расчетное значение попадает в интервал (2,7 – 3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна.
· Проверка равенства нулю математического ожидания уровней ряда остатков.
В нашем случае 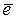 = 0, поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
= 0, поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
В табл. 4.3.18собраны данные анализа ряда остатков.
Таблица 4.3.18. Анализ ряда остатков
| Проверяемое свойство | Используемые статистики | Граница | Вывод | |||
| наименование | значение | нижняя | верхняя | |||
| Независимость | d-критерий Дарбина–Уотсона r (1) – коэффициент автокорреляции | d =2,12 dn =4-2,21=1,88 | 0,98 | 1,36 0,36 | адекватна | |
| Случайность | Критерий пиков (поворотных точек) | 5 > 4 | адекватна | |||
| Нормальность | RS-критерий | 3,383 | 2,6 | 2,7 | адекватна | |
Среднее 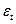 = 0? = 0?
| t-статистика Стьюдента | 0,000 | -2,179 | 2,179 | адекватна | |
| Вывод: Модель статистически адекватна | ||||||
2.2) Оценка точности
Для оценки точности модели вычислим среднюю относительную ошибку аппроксимации 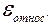
Таблица 4.3.19.
| Номер наблюдения | 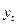
| 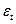
| 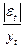
|
| 4,96 | 0,110 | ||
| -1,85 | 0,046 | ||
| -0,66 | 0,015 | ||
| 2,53 | 0,053 | ||
| -5,28 | 0,126 | ||
| -2,09 | 0,045 | ||
| 0,09 | 0,002 | ||
| 2,28 | 0,042 | ||
| -4,53 | 0,091 | ||
| 0,66 | 0,012 | ||
| 1,85 | 0,031 | ||
| 2,04 | 0,033 |
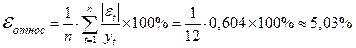
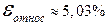 - хороший уровень точности модели.
- хороший уровень точности модели.
3) Построить точечный и интервальный прогнозы на три шага вперед
Для вычисления точечного прогноза в построенную модель подставляем соответствующие значения фактора 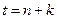 :
:
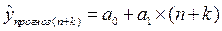
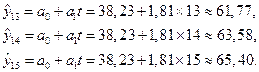
Для построения интервального прогноза рассчитаем доверительный интервал. Примем значение уровня значимости α = 0,1, следовательно, доверительная вероятность равна 90%, а критерий Стьюдента при 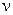 = n –2 =11 равен 1,812. Ширину доверительного интервала вычислим по формуле (3.10):
= n –2 =11 равен 1,812. Ширину доверительного интервала вычислим по формуле (3.10):
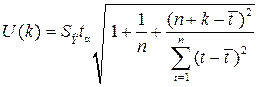 ,
,
где 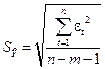 =3,177
=3,177 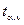 = 1,812,
= 1,812, 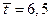 ,
, 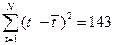 (находим из табл. 4.3.15),
(находим из табл. 4.3.15),
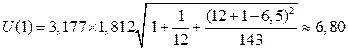 ,
,
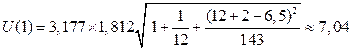 ,
,
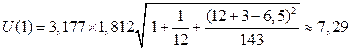 .
.
.
Далее вычисляем верхнюю и нижнюю границы прогноза (см. табл. 4.3.20).
Верхняя граница = 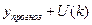
Нижняя граница = 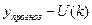
Таблица 4.3.20.
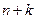
| 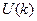
| Прогноз | Верхняя граница | Нижняя граница |
| U1=6,80 | 61,77 | 68,57 | 54,97 | |
| U2=7,04 | 63,58 | 70,62 | 56,55 | |
| U3=7,29 | 65,40 | 72,69 | 58,10 |
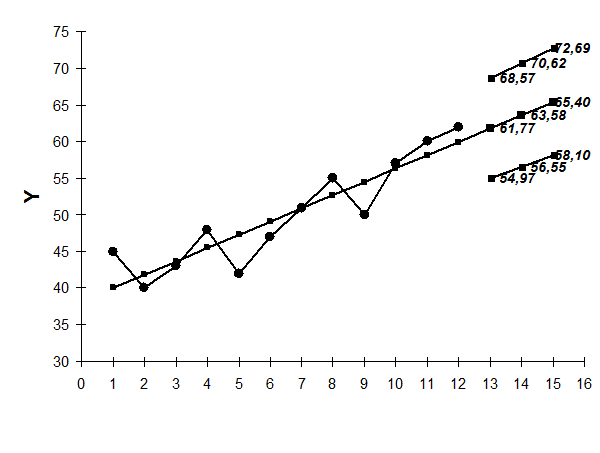
Рис. 3.4.15. Результаты моделирования и прогнозирования
Ответ
1) Модель имеет вид Y = 38.23 +1.81 t.
2) Размеры платежей составят 61,77, 63,58, 65,40 тыс. руб.
3) Денежных средств в объеме 120 тыс. руб. на финансирование этого инвестиционного проекта на 3 последующие месяца будет недостаточно, поэтому нужно либо изыскать дополнительные средства, либо отказаться от этого проекта.
[1] Экстраполяция - это распространение выявленных при анализе рядов динамики закономерностей развития изучаемого объекта на будущее (при предположении, что выявленная закономерность, выступающая в качестве базы прогнозирования, сохраняется и в дальнейшем).
[2] Источник - "Краткосрочные экономические показатели. РФ". Госкомстат, Москва. (https://www.gks.ru/)
[3] табличное значение t кр можно получить с помощью функции EXCEL СТЬЮДРАСПОБР.
[4] В фактически действующих ценах соответствующих лет.
Источник - "Краткосрочные экономические показатели РФ". Госкомстат, Москва.
[5] Значение можно получить с помощью функции Excel СТЬЮДРАСПОБР.
 2014-01-25
2014-01-25 873
873








