Определение 1. Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную 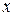 , искомую функцию
, искомую функцию 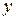 и ее производную первого порядка
и ее производную первого порядка 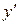 , то есть
, то есть
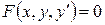 . (1)
. (1)
Если уравнение (1) можно разрешить относительно 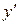 , то его записывают в виде
, то его записывают в виде
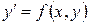 . (2)
. (2)
Обозначим через 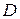 множество точек плоскости
множество точек плоскости 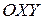 , на котором функция
, на котором функция 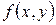 определена.
определена.
Рассмотрим геометрический смысл уравнения (2).
Производная функции 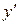 представляет собой угловой коэффициент (тангенс угла наклона) касательной к кривой
представляет собой угловой коэффициент (тангенс угла наклона) касательной к кривой 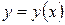 в точке с абсциссой
в точке с абсциссой 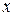 . Следовательно, уравнение (2) устанавливает связь (зависимость) между координатами каждой точке
. Следовательно, уравнение (2) устанавливает связь (зависимость) между координатами каждой точке 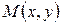 плоскости
плоскости 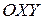 и угловым коэффициентом
и угловым коэффициентом 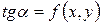 касательной к интегральной кривой
касательной к интегральной кривой 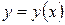 , проходящей через эту точку. Если указать это направление единичным вектором, проходящим через точку
, проходящей через эту точку. Если указать это направление единичным вектором, проходящим через точку 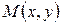 , то будет получено поле направлений.
, то будет получено поле направлений.
Определение 2. Кривая, во всех точках которой направление поля одинаково, называется изоклиной.
Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить 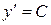 , то есть
, то есть 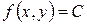 .
.
Пример 1. С помощью изоклин начертить вид интегральных кривых уравнения 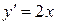 .
.
Решение:
1. Уравнение изоклин этого дифференциального уравнения будет 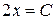 , то есть изоклинами здесь будут прямые, параллельные оси
, то есть изоклинами здесь будут прямые, параллельные оси 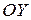
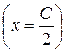 .
.
2. В точках прямых проведем отрезки, образующие с осью 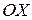 один и тот же угол
один и тот же угол 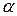 , тангенс которого равен
, тангенс которого равен 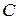 , то есть
, то есть
при 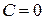 :
: 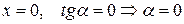 ;
;
при 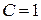 :
: 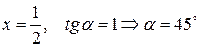 ;
;
при 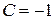 :
: 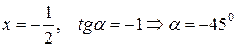 ;
;
при 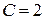 :
: 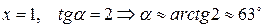 .
.
3. Построив четыре изоклины и отметив на каждой из них ряд стрелочек, наклоненных к оси 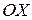 под определенным углом, по их направлениям строим линии. Они представляют собой семейство парабол.
под определенным углом, по их направлениям строим линии. Они представляют собой семейство парабол.
Решить уравнение (2) – значит найти семейство кривых, отвечающих заданному полю направлений.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:
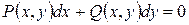 , (3)
, (3)
где 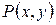 и
и 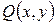 - известные функции.
- известные функции.
Уравнение (3) удобно тем, что переменные 
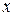 и
и 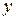 в нем равноправны, то есть любую из них можно рассматривать как функцию другой. Отметим, что от одного вида записи дифференциального уравнения можно перейти к другому.
в нем равноправны, то есть любую из них можно рассматривать как функцию другой. Отметим, что от одного вида записи дифференциального уравнения можно перейти к другому.
Интегрирование дифференциального уравнения в общем случае приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами).
Пример 2. Решением уравнения 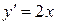 являются функции
являются функции 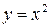 ,
, 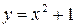 ,
, 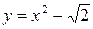 и вообще
и вообще 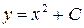 , где
, где 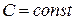 .
.
Для того, чтобы решение дифференциального уравнения приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.
Определение 3. Начальным условием называется условие, при котором заданному значению независимой переменной 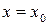 должно соответствовать заданное значение функции
должно соответствовать заданное значение функции 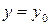 .
.
Начальное условие записывается в виде:
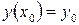 или
или 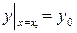 (4)
(4)
Задача отыскания решения дифференциального уравнения, удовлетворяющего начальному условию (4), называется задачей Коши.
Теорема (существования и единственности решения задачи Коши). Если в уравнении (2) функция 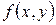 и ее частная производная
и ее частная производная 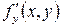 непрерывны в некоторой области
непрерывны в некоторой области 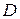 , содержащей точку
, содержащей точку 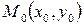 , то существует единственное решение
, то существует единственное решение 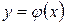 этого уравнения, удовлетворяющее начальному условию (4).
этого уравнения, удовлетворяющее начальному условию (4).
Геометрическое представление задачи Коши состоит в том, что при выполнении ее условий существует единственная интегральная кривая дифференциального уравнения, проходящая через точку 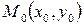 .
.
Постановка задачи Коши. Для данной точки 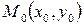 найти такую функцию
найти такую функцию 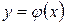 , чтобы она была решением уравнения (2) и ее график проходил через заданную точку
, чтобы она была решением уравнения (2) и ее график проходил через заданную точку 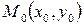 .
.
Следовательно, решение задачи для уравнения (2) сводится к нахождению частного решения для этого уравнения. При этом в соотношение 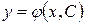 вместо
вместо 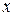 и
и 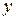 надо подставить начальные значения
надо подставить начальные значения 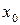 и
и 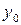 , то есть получить выражение
, то есть получить выражение 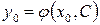 . Отсюда легко получить
. Отсюда легко получить 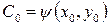 . Подставляя это значение
. Подставляя это значение 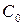 в формулу общего решения получим
в формулу общего решения получим 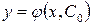 . Это и есть искомое решение задачи Коши. Других решений нет.
. Это и есть искомое решение задачи Коши. Других решений нет.
Пример 3. Рассмотрим дифференциальное уравнение 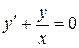 , общее решение которого имеет вид
, общее решение которого имеет вид 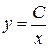 . Задача Коши: найти решение дифференциального уравнения, удовлетворяющее начальным условиям
. Задача Коши: найти решение дифференциального уравнения, удовлетворяющее начальным условиям 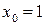 ,
, 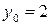 .
.
Решение: Подставляя в общее решение значения 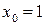 и
и 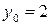 получим
получим 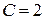 . При этом значении из общего решения получим
. При этом значении из общего решения получим 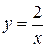 . Это есть аналитическое решение задачи Коши. С точки зрения геометрии найдена интегральная кривая, проходящая через точку с координатами
. Это есть аналитическое решение задачи Коши. С точки зрения геометрии найдена интегральная кривая, проходящая через точку с координатами 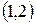 .
.
§ 3. Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является уравнение вида:
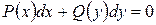 (1)
(1)
В нем одно слагаемое зависит только от 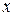 , а другое – от
, а другое – от 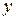 . Иногда такие дифференциальные уравнения называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получим
. Иногда такие дифференциальные уравнения называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получим 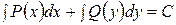 – его общий интеграл.
– его общий интеграл.
Пример 1. Найти общий интеграл уравнения 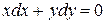 .
.
Решение: 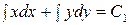

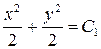 . Обозначим
. Обозначим 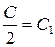 , тогда
, тогда 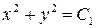 – общий интеграл дифференциального уравнения.
– общий интеграл дифференциального уравнения.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид
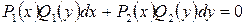 (2)
(2)
Особенность уравнения (2) в том, что коэффициенты при 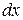 и
и 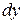 представляют собой произведения двух функций (чисел), одна из которых зависит только от
представляют собой произведения двух функций (чисел), одна из которых зависит только от 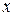 , другая – только от
, другая – только от 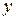 .
.
Для решения такого уравнения, его следует преобразовать его к виду, в котором дифференциал и функция переменной 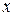 окажутся в одной части равенства, а переменной
окажутся в одной части равенства, а переменной 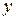 – в другой. То есть необходимо почленно разделить уравнение (2) на
– в другой. То есть необходимо почленно разделить уравнение (2) на 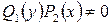 . При этом получим
. При этом получим
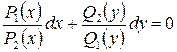 ,
,
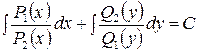 - общий интеграл.
- общий интеграл.
Пример 2. Решить уравнение 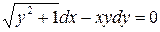 .
.
Решение:
1. Разделим обе части этого уравнения на 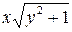 (при
(при 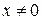 ):
):
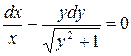 .
.
2. Проинтегрируем обе части 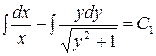 .
.
3. Вычислим второй интеграл отдельно методом подстановки
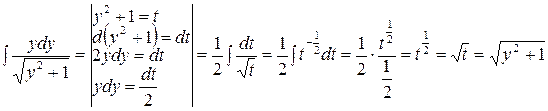 .
.
4. 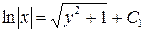

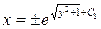

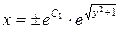 или
или 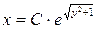 , где
, где 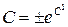
 2014-01-25
2014-01-25 1882
1882
