2014-01-25
735
Замечание 1. При выполнении почленного деления дифференциального уравнения на могут быть потеряны некоторые решения. Если эти решения не входят в общее решение ни при каких числовых значениях произвольной постоянной, то они представляют собой особые решения.
Поэтому следует отдельно решить уравнение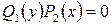 
и установить те решения дифференциального уравнения, которые не могут быть получены из общего решения, то есть особые решения.
Пример 3. Решить уравнение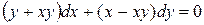 
.
Решение: 
1. Вынесем общие множители за скобки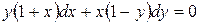 
.
2. Разделим обе части уравнения на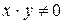 
: 
.
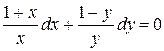3. Проинтегрируем обе части:
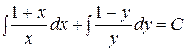
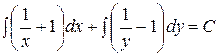
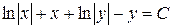
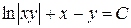- общий интеграл.
4. Здесь уравнение 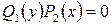имеет вид 
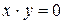. Его решения 
, 
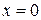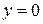являются решениями данного дифференциального уравнения (можно проверить подстановкой в уравнение), но не входят в общий интеграл (так как по определению логарифма 
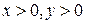). Следовательно решения 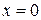, 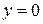являются особыми.
Замечание 2. Уравнение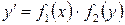 
также сводится к уравнению с разделяющимися переменными. Для этого достаточно положить 
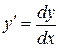и разделить переменные.
Пример 4. Решить уравнение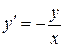 
, удовлетворяющее условию 
.
|
|
|
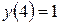Решение:
1. Так как 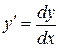, то 
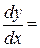
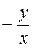или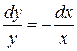 
.
2. Проинтегрируем обе части уравнения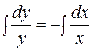 
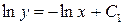
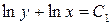
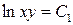
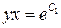
при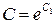 
получим 
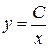- общее решение.
3. Найдем частное решение при :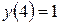 
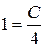
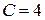
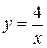- частное решение.
Дифференциальное уравнение первого порядка называется однородным, если оно может быть представлено в виде:
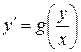, (1)
где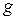 
- некоторая функция одной переменной.
Например, уравнение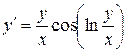 
однородное.
Понятие однородного дифференциального уравнения связано с однородными функциями. Функция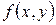 
называется однородной степени 
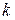(по переменным 
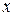и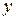 
), если для произвольного числа 
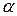выполняется равенство:
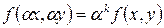. (2)
Пример 1. Выяснить, являются ли однородными следующие функции:
а)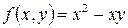 
; б) 
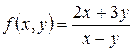; в)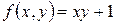 
.
Решение:
а) Так как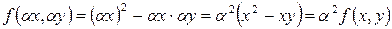 
, то данная функция является однородной степени 2.
б) Так как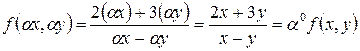 
, то данная функция является однородной степени 0.
в) Так как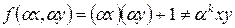 
ни при каком значении 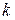, то данная функция не является однородной.
Если функция 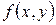является однородной степени 0, то уравнение 
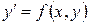может быть сведено к однородному.
Рассмотрим способ решения дифференциального уравнения (1).
Однородное уравнение (1) преобразуется в уравнение с разделяющимися переменными при помощи подстановки
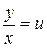или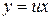 
,
при этом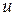 
называется вспомогательной функцией.
Действительно, так как 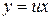, то по правилу дифференцирования произведения получим: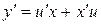 
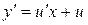, поэтому уравнение (1) приобретает следующий вид 
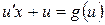, откуда получим
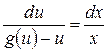(3)
Пример 2. Решить уравнение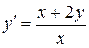 
.
Решение:
1. Так как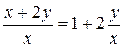 
, то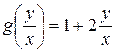 
.
2. Положим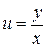 
, тогда 
.
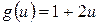3. Так как 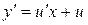, то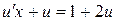 
.
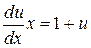
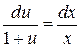4. Проинтегрировав обе части получим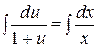 
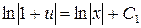
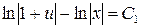
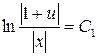
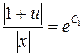
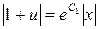
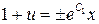
если обозначить 
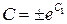, то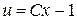 
.
5. Возвращаемся к старой переменной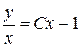 
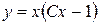- общее решение.
