Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде
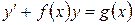 , (1)
, (1)
где 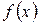 и
и 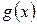 – некоторые (непрерывные) функции переменной
– некоторые (непрерывные) функции переменной 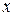 .
.
В случае, когда функция 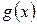 тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.
тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.
Особенность дифференциального уравнения (1) состоит в том, что искомая функция 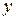 и производная
и производная 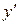 входят в уравнение в некоторой степени, не перемножаясь между собой.
входят в уравнение в некоторой степени, не перемножаясь между собой.
Одним из возможных способов решения линейного уравнения (1) является метод Бернулли.
Метод Бернулли. Решение уравнения (1) ищется в виде произведения двух функций, то есть с помощью подстановки 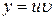 , где
, где 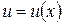 и
и 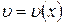 – неизвестные функции от переменной
– неизвестные функции от переменной 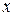 , причем одна из них произвольна (но не равна нулю). Тогда по правилу дифференцирования произведения
, причем одна из них произвольна (но не равна нулю). Тогда по правилу дифференцирования произведения 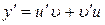 . Подставив
. Подставив 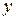 и
и 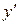 в уравнение (1), получим
в уравнение (1), получим
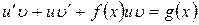
или
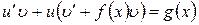 . (2)
. (2)
Подберем функцию 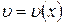 так, чтобы выражение в скобках было равно нулю, то есть решим дифференциальное уравнение
так, чтобы выражение в скобках было равно нулю, то есть решим дифференциальное уравнение 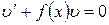 . Получим
. Получим 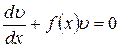

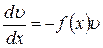

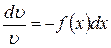 . Интегрируя почленно получим:
. Интегрируя почленно получим: 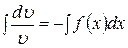

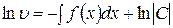 .
.
Ввиду свободы выбора функции 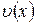 , можно принять
, можно принять 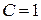 . Тогда
. Тогда  так как
так как 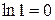

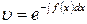 .
.
Подставляя найденную функцию 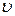 в уравнение
в уравнение 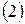 получаем
получаем 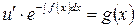 .
.
Получено уравнение с разделяющимися переменными. Решим его: 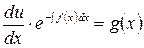

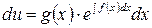

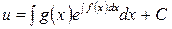 .
.
Возвращаясь к переменной 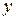 , получаем:
, получаем:
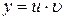

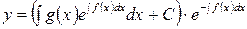 - решение исходного уравнения (1).
- решение исходного уравнения (1).
Пример 1. Решить уравнение 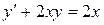 .
.
Решение:
1. Полагаем 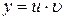 . Тогда
. Тогда 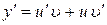 .
.
2. Подставим в уравнение 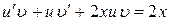 . Сгруппируем относительно
. Сгруппируем относительно 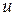 :
: 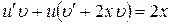 .
.
3. Приравняем скобку к нулю и найдем 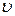 , то есть
, то есть 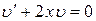

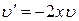

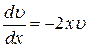

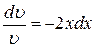

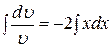

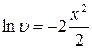

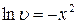

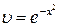 .
.
4. Теперь решаем уравнение 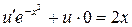 или
или 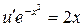 . Так как
. Так как 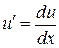 , то
, то 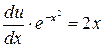 . Это уравнение с разделяющимися переменными. Решим его:
. Это уравнение с разделяющимися переменными. Решим его: 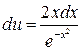

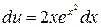

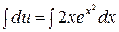 .
.
5. Найдем второй интеграл отдельно методом подстановки: 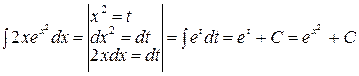
6. Таким образом, общее решение исходного уравнения примет вид: 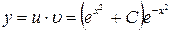 , то есть
, то есть 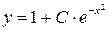 .
.
Иногда в качестве независимой переменной удобнее выбрать переменную 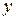 , а в качестве зависимой переменную
, а в качестве зависимой переменную 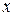 .
.
Пример 2. Решить уравнение 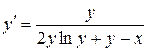 .
.
Решение:
1. Будем считать 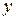 независимой переменной, а
независимой переменной, а 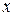 зависимой, тогда с учетом того, что
зависимой, тогда с учетом того, что 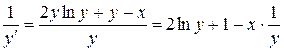 и
и 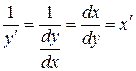 получим
получим 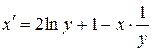 уравнение, которое можно привести к линейному
уравнение, которое можно привести к линейному 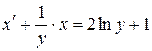 .
.
2. Пусть 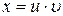 , тогда
, тогда 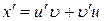 . Подставим в последнее уравнение
. Подставим в последнее уравнение 
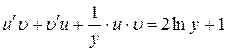 . Сгруппируем слагаемые с
. Сгруппируем слагаемые с 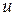 и вынесем
и вынесем 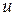 за скобки
за скобки 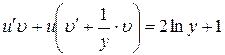 .
.
3. Найдем 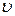 , для чего приравняем скобку к нулю
, для чего приравняем скобку к нулю 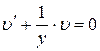

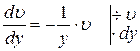

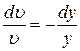

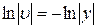

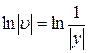

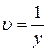 .
.
4. Найдем 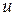 :
: 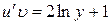

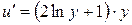

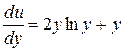

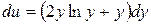 . Проинтегрируем обе части:
. Проинтегрируем обе части: 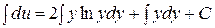 . Вычислим первый интеграл в правой части отдельно интегрированием по частям:
. Вычислим первый интеграл в правой части отдельно интегрированием по частям: 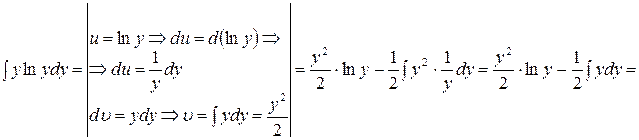
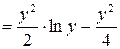 . Подставим найденное значение в уравнение:
. Подставим найденное значение в уравнение: 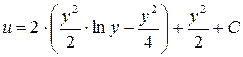

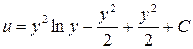

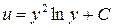 .
.
5. С учетом того, что 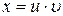 получим
получим 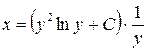 - общее решение.
- общее решение.
Для решения линейных дифференциальных уравнений применяется так же метод вариации произвольных постоянных или метод Лагранжа.
Метод Лагранжа. Общее решение неоднородного уравнения (1) можно найти при помощи общего решения соответствующего однородного уравнения, то есть
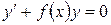 . (3)
. (3)
Уравнение (3) с разделяющимися переменными: 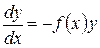

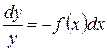

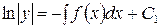

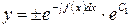

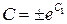

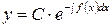 . (4)
. (4)
Для решения исходного уравнения (1) полагаем в (4), что 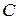 является некоторой функцией от переменной
является некоторой функцией от переменной 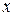 , то есть
, то есть 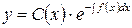 . Для нахождения функции
. Для нахождения функции 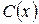 подставляем это значение
подставляем это значение 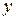 в уравнение (1):
в уравнение (1): 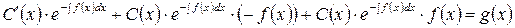


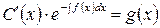

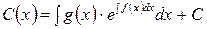 .
.
Подставляя последнее значение 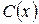 в уравнение (4), находим
в уравнение (4), находим 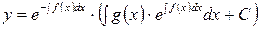 - общее решение уравнения (1).
- общее решение уравнения (1).
Пример 3. Проинтегрировать уравнение 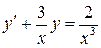 .
.
Решение:
 2014-01-25
2014-01-25 1773
1773
