Неравенство Чебышева

Случайный характер величины проявляется в том, что нельзя предвидеть, какое именно из своих значений она примет в итоге испытания. Это зависит от многих случайных причин, учесть которые мы не в состоянии. Поскольку о каждой случайной величине мы располагаем весьма скромными сведениями, то оказалось бы, что вряд ли можно установить закономерности поведения суммы достаточно большого числа случайных величин. В действительности - это не так.

Оказывается, что совокупное действие многих случайных причин может приводить к результату, почти не зависящему от случая.

Так, при рассмотрении суммы большого числа случайных величин и их средних арифметических мы обнаруживаем, что частичное погашение отклонений при сложении вызывает уменьшение рассеяния средней арифметической и дает возможность предсказать ее поведение при неограниченном увеличении числа слагаемых, т.е. поведение суммы большого числа случайных величин почти утрачивает случайный характер и становится закономерным; здесь необходимое прокладывает себе дорогу сквозь множество случайностей.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, т.к. позволяет предвидеть ход явлений.

Закономерности такого рода и условия их возникновения составляют содержание ряда важных теорем, получивших общее название " закона больших чисел".

В исследовании этих вопросов значит роль сыграли работы выдающегося русского математика, академика П.Л. Чебышева (1821-1894) и его учеников.

Закон больших чисел играет важную роль в практическом применении теории вероятности.

Свойство случайных величин вести себя (при определенных условиях) практически как не случайные позволяет уверенно оперировать с этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.

Неравенство Чебышева оценивает вероятность того, что отклонение случайных величин х от М[x] не превзойдет заданное положительное число e.. Для любой случайной величины справедлива

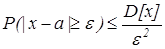заданное положительное число (" e > 0)

Эта вероятность тем меньше, чем меньше дисперсия, в качестве характеристики рассеяния. Приведем доказательство для непрерывных случайных величин, известно, что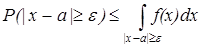

f(x) – плотность распределения.

Интеграл в правой части распространяется как интервалы от -∞ до а – e и от а – e до ∞. В этих интервалах имеет место следующее неравенство. Возьмем данный интервал и возведем в квадрат 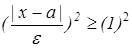, так как f(x) – неотрицательная функция f(x) > 0 умножим обе части на f(x) и проинтегрируем.

,

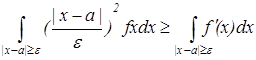В силу положительности подинтегральной функции можно перейти к интегралу: -∞; +∞

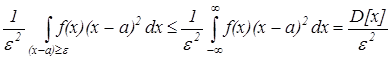(1)

другая формула неравенства (1). Если (х-а) < e, то

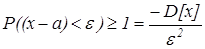(2)