Для центральной и предельной теоремы и для решения ряда других задач теории вероятности весьма удобным оказался метод характеристических функций, разработанный А.М. Ляпуновым.
Характеристической функцией 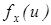 случайной величины x называется математическое ожидание величины eiux:
случайной величины x называется математическое ожидание величины eiux:
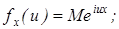
где u - действительный параметр; i - мнимая единица.
а)Для непрерывной случайной величины характеристическая функция совпадает с преобразованием Фурье от плотности распределения вероятностей P (x):
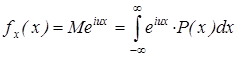 ;
;
Отсюда сразу следует оценка характеристической функции
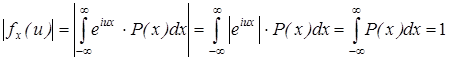 , т.е.
, т.е. 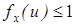 .
.
б)Для дискретной случайной величины
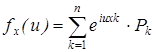 .
.
Рассмотрим некоторые свойства характеристических функций
I. Характеристическая функция однозначно определяет распределение вероятностей случайной величины.
Другими словами две случайные величины имеют одинаковые характеристические функции, то они имеют также и одинаковые распределения.
II. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
Доказательство: Независимость случайных величин x и y влечет за собой независимость величин eiux и eiuy, поэтому 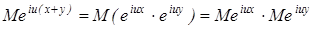 , т.е.:
, т.е.:
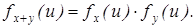
Таким образом, при изучении сумм независимых случайных величин проще оперировать с характеристическими функциями (которые при этом перемножаются), чем с плотностями (которые свертываются).
Конечно, переход к характеристическим функциям и обратно требует умения оперировать с преобразованиями Фурье (существуют таблицы преобразований Фурье).
III. При умножении случайной величины x на число C характеристическая функция преобразуется следующим образом:
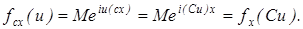
Если случайная величина x имеет всюду непрерывную плотность распределения P (x), то эта плотность может быть выражена через характеристическую функцию 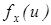 с помощью обратного преобразования Фурье:
с помощью обратного преобразования Фурье:
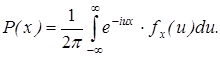
 2014-01-25
2014-01-25 1481
1481








