2014-01-25
920
Некоторых элементарных функций
Основные разложения в ряд Маклорена
Для разложения функции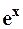 
в ряд Маклорена находим последовательно производные и вычисляем значение функции и её производных в точке 
.
, 
, 
,...., 
, 
,...
, 
, 
,..., 
, 
,...
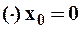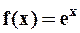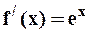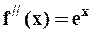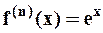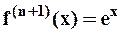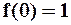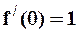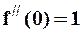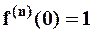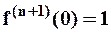По формуле Маклорена имеем:
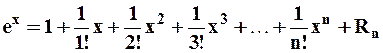, где
, 
.
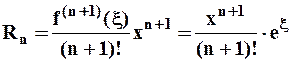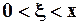Кроме того, составим ряд Маклорена для функции :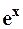
.
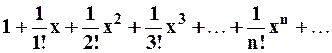Как нетрудно установить, полученный степенной ряд сходится на всей числовой оси:
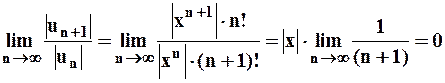, если 
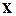– любое фиксированное число.
А тогда, по необходимому признаку сходимости ряда общий член ряда стремится к нулю при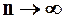 
, т.е. 
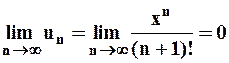, а тогда и 
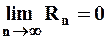, так как для всех фиксированных значений 
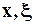величина 
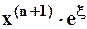– есть величина конечная.
Итак, сумма такого ряда Маклорена есть сама функция, для которой этот ряд построен, т.е.
, 
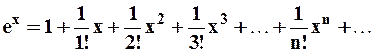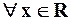
Если положить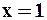 
, то получим: 
.
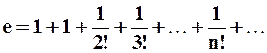2. Разложение синуса и косинуса.
Пусть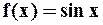 
. Тогда имеем:
, 
, 
, 
, 
,....
, , 
, 
, 
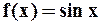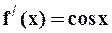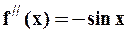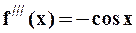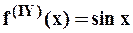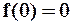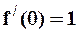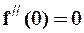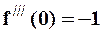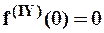,... и т.д.
Поэтому ряд Маклорена для функции 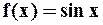имеет вид:
.
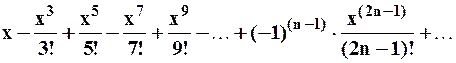Этот ряд действительно имеет своей суммой функцию 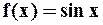при любом значении 
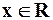, так как остаточный член 
формулы Маклорена стремится к нулю при 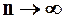. В самом деле: 
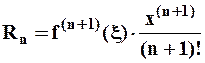, где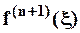 
– есть функция 
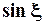либо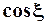 
со знаком “+” или “–”, следовательно 
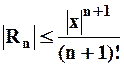, но правая часть данного неравенства является общим членом сходящегося при любых значениях 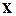ряда Маклорена для функции 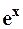, поэтому она (правая часть) стремится к нулю при 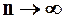для любых фиксированных 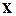. Т.е. 
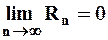. И тогда сумма полученного ряда равна самой функции: 
, .
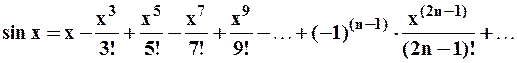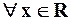Аналогично получаем:
, .
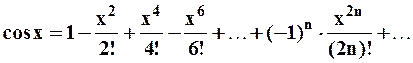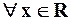Из представления функций в виде рядов Маклорена видны характерные степени “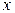
” для чётной функции – чётные степени, для нечётной функции – нечётные степени.
Замечание. Последнее представление функции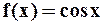 
можно было бы получить из представления в виде ряда Маклорена для 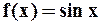путём почленного дифференцирования.
Полученные разложения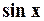 
и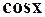 
удобны для вычисления приближённых значени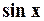й и 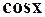. Причём для малых значений 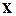достаточно взять немного членов разложения, чтобы достичь требуемую точность вычисления.
