Разложим в ряд Маклорена функцию: 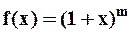 , где
, где 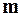 – любое действительное число. Получим значение функции и её производных:
– любое действительное число. Получим значение функции и её производных:
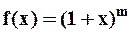 ,
, 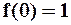 .
.
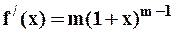 ,
, 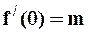 .
.
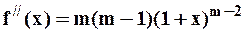 ,
, 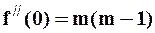 .
.
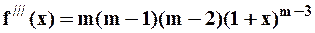 ,
, 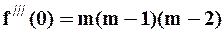 .
.
............................................................................................
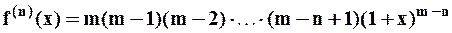 ,
, 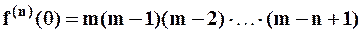 .
.
...........................................................................................
Поэтому ряд Маклорена функции 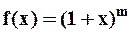 имеет вид:
имеет вид:
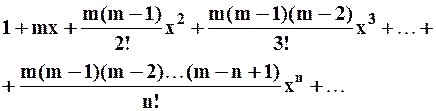
Установим область сходимости данного ряда:
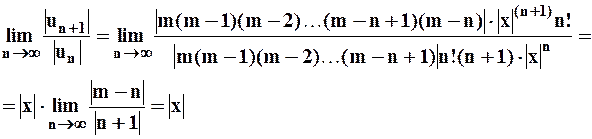
Если 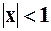 , то данный ряд будет сходящимся, т. е. Интервал сходимости данного ряда есть
, то данный ряд будет сходящимся, т. е. Интервал сходимости данного ряда есть 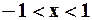 . Доказательство того факта, что остаточный член формулы Маклорена стремится к нулю здесь приводить не будем. Итак, имеем, что при
. Доказательство того факта, что остаточный член формулы Маклорена стремится к нулю здесь приводить не будем. Итак, имеем, что при 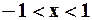 верно равенство:
верно равенство:
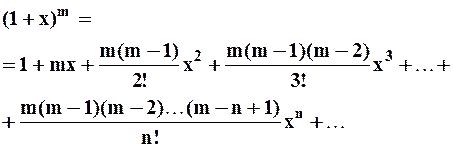
Если 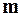 – целое положительное число, то ряд содержит всего
– целое положительное число, то ряд содержит всего 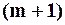 слагаемых и превращается в формулу бинома Ньютона.
слагаемых и превращается в формулу бинома Ньютона.
Рассмотрим ряд:
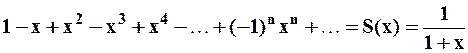 , т.к. это бесконечно убывающая геометрическая прогрессия при
, т.к. это бесконечно убывающая геометрическая прогрессия при 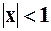 , со знаменателем
, со знаменателем 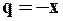 .
.
С другой стороны: 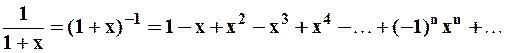 – это биноминальный ряд и он сходится к самой функции при
– это биноминальный ряд и он сходится к самой функции при 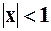 .
.
При  биноминальный ряд расходится.
биноминальный ряд расходится.
Аналогично можно получить разложение функции 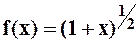 в биноминальный ряд:
в биноминальный ряд: 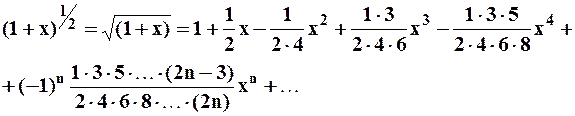 ,
,
который имеет место при 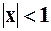 .
.
 2014-01-25
2014-01-25 817
817








