Пример 2. (два раза мы применили правило Лопиталя для

Пример 1.

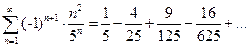
а)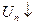

б)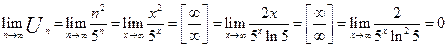

(два раза мы применили правило Лопиталя для ).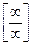

Т.е. знакочередующийся ряд сходится по признаку Лейбница.

Тогда 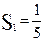; 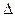- абсолютная погрешность,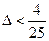

;

;

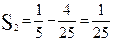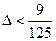
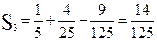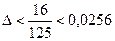
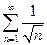
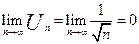- необходимый признак сходимости выполнен

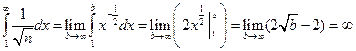
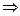интеграл расходится по интегральному признаку Коши.

;

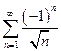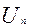убывают, 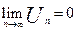, выполняются условия т. Лейбница – значит, ряд сходится.