2014-01-25
941
Знакочередующиеся ряды.
Пример 11.
Пример 10.
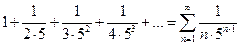
Т.к. 
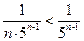, а ряд 
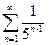сходится по признаку Даламбера, то
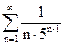тоже сходится по признаку сравнения.
Найти сумму ряда
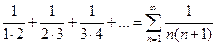
Т.к.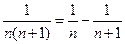 
, то исходный ряд можно представить в виде:
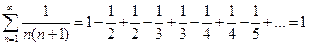
Определение: Ряды вида
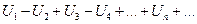(3)
где знаки строго чередуются, называются знакочередующимися.
Если в знакочередующемся ряде (3):
а) члены ряда убывают, т.е.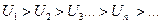 
б) общий член стремится к нулю, при n стремящимся к бесконечности, т.е.
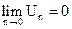, то ряд (3) сходится, его сумма положительна и не превышает первого члена ряда.
Доказательство:
Рассмотрим частную сумму первых n=2m членов ряда. Представим её в виде:
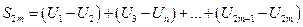
>0 >0 >0
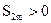и возрастает с возрастанием m; с другой стороны,
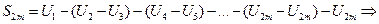
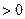
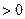
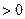
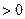
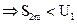
Т.е. получим, что частные суммы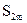 
возрастают и ограничены сверху числом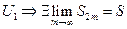 
Для нечетных частичных сумм имеем.
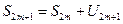
Т.к.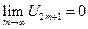 
, то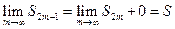 
Вывод: Ошибка при замене суммы сходящегося знакочередующегося ряда с убывающими по абсолютной величине членами суммой нескольких его первых членов меньше абсолютного значения первого из отброшенных членов.
