2014-01-25
714
Пример 7.
Пример 6.
Пример 5.
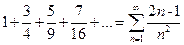
Т.к.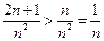 
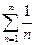- расходится, то 
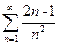тоже расходится по признаку сравнения.
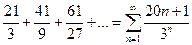
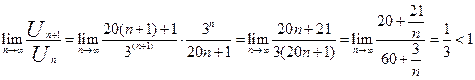
-ряд сходится по признаку Даламбера.
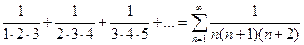
Т.к.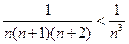 
,
а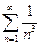 
- сходится, по интегральному признаку Коши.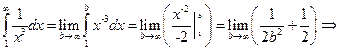 
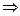, то ряд 
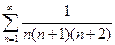тоже сходится по признаку сравнения.
Определение: Ряд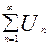 
(4) называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Теорема 1:
Если знакопеременный ряд (4) таков, что ряд, составленный из абсолютных значений его членов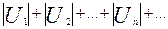 
(4.1) сходится, то ряд (4) называется абсолютно сходящимся
Теорема 2:
Если знакопеременный ряд (4) сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов.
Теорема 3:
Если (4) сходится условно, то какое бы число А мы ни задали можно так переставить члены ряда, что его сумма в точности будет равна А.
Можно даже так переставить члены этого ряда, что ряд, полученный после перестановки, будет расходиться.
