2014-01-25
761
Пример 5
Пример 4
Найти предел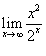 
.
Решение.
Используя правило Лопиталя, можно записать
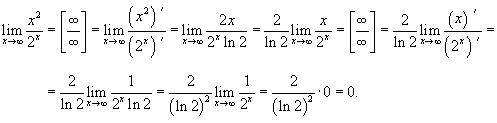
Найти предел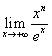 
.
Решение.
Предел имеет неопределенность типа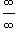 
. Применяем правило Лопиталя n раз.
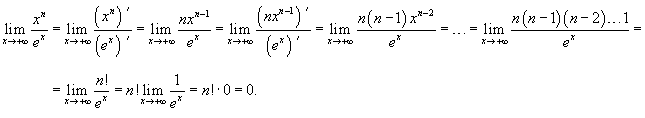
Рассмотрим ряд важных теорем, которые полезны при исследовании функции.
Определение. Точка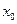 
называется точкой локального максимума (минимума), а значение функции в ней – локальным максимумом (минимумом) функции 
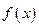, если существует окрестность 
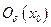такая, что для любой точки 
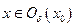будет справедливо неравенство 
.
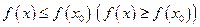Определение. Точки локального максимума и минимума называются точками локального экстремума, а значение функции в них – локальными экстремумами функции.
Пример. Точка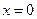 
является точкой локального максимума, а точка 
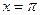точкой локального минимума для функции 
.
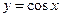Определение. Точка 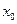называется внутренней точкой промежутка 
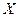, если она принадлежит ему вместе со своей окрестностью.
Теорема (Ферма). Если функция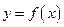 
определенная на промежутке 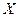, дифференцируема в точке внутреннего экстремума 
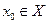, то ее производная в этой точке равна нулю: 
.
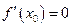Замечание. Теорема Ферма дает необходимое условие внутреннего экстремума дифференцируемой функции, это условие не является достаточным.
Пример. У функции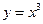 
в нуле производная обращается в нуль, но 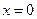не является точкой локального экстремума этой функции.
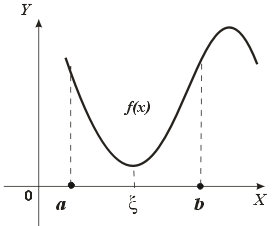
Теорема (Ролля). Если функция 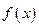определена и непрерывна на отрезке 
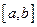, дифференцируема на интервале 
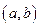и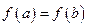 
, то найдется точка 
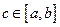, в которой 
.
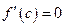Теорема (Лагранжа о конечном приращении ). Если функция 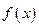определена и непрерывна на отрезке 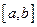и дифференцируема на интервале 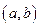, то найдется точка 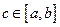такая, что
.
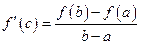Теорема (Коши о конечных приращениях). Пусть функции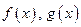 
непрерывны на отрезке 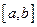и дифференцируемы на интервале 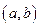, причем 
.
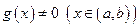Тогда найдется точка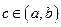 
такая, что
.
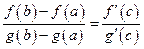Теорема (о монотонности функции). Пусть функция 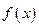определена и дифференцируема на некотором интервале 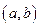, и пусть производная 
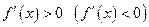на 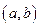. Тогда функция возрастает (убывает) на этом интервале.
Теорема (о постоянной функции). Непрерывная на интервале 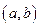функция постоянна на нем тогда и только тогда, когда ее производная равна нулю на этом интервале.
