Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
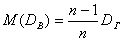 ,
,
где DГ – истинное значение дисперсии генеральной совокупности.
Для исправления выборочной дисперсии достаточно умножить ее на дробь 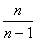
В качестве оценки генеральной дисперсии принимают исправленную дисперсию s ², вычисляемую по формуле
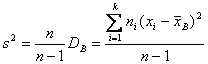 .
.
Такая оценка будет являться несмещенной. Ей соответствует исправленное среднее квадратическое отклонение
 .
.
Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение
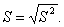
Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n < 30.
Пример
| xi | ||||
| n1 |
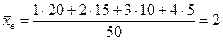
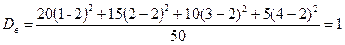
Коэффициент вариации применяют для сравнения вариации признаков сильно отличающихся по величине, или имеющих разные единицы измерения (разные наименования). 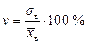
На практике считают, что если 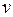 < 33 %, то совокупность однородная.
< 33 %, то совокупность однородная.
Модой M0 называют варианту, которая имеет наибольшую частоту.
| варианта | ||||
| частота |
мода равна 7.
Медианой тe называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т. е. 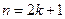 , то
, то 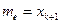 , при четном п = 2k медиана
, при четном п = 2k медиана 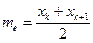
Например, для ряда 2 3 5 6 7 медиана равна 5; для ряда 2 3 5 6 7 9
медиана равна 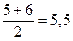
 2014-01-25
2014-01-25 3442
3442








