Формы рядов распределения. Расчет показателей центра распределения

Тема 5. Анализ рядов распределения

Контрольные вопросы

1. Что такое абсолютные величины, в каких единицах они выражаются?

2. Каковы формы выражения относительных величин?

3. Каковы общие принципы построения и использования абсолютных и относительных величин в экономическом анализе?

4. Какая существует взаимосвязь между относительными величинами планового задания, выполнения плана и динамики?

5. Кто называется базой (основанием) для исчисления относительной величины?

6. В чем различие между относительными величинами структуры и координации?

7. В каких случаях целесообразно выражать относительные величины в промиллях?

План

1. Формы рядов распределения. Расчет показателей центра распределения.

2. Измерение и оценка вариации.

2.1. Абсолютные показатели вариации.

2.2. Относительные показатели вариации.

3. Методы определения и свойства дисперсии.

4. Оценка меры асимметрии,

Разнообразие статистических совокупностей обуславливает и многообразие рядов распределения, которые характеризуются прежде всего формой соотношения частот и значений варьирующего признака. По своей форме ряды распределения бывают одно-, двух- и многовершинными. Распределения качественно однородных совокупностей преимущественно одновершинные. Среди них выделяют симметричные и асимметричные, остро- и плосковершинные ряды распределения.

Для характеристики центра распределения применяются: средняя арифметическая, мода и медиана. В симметричном распределении .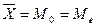

Порядок определения средней арифметической приведен в теме 4. Рассмотрим особенности расчета моды и медианы дискретных и вариационных рядов.

Модой называется наиболее часто встречающееся значение признака.

В дискретном ряду мода – это варианта с наибольшей частотой.

В интервальном ряду модой приближенно считают центральный вариант модального интервала, т.е. того интервала, который имеет наибольшую частоту. В пределах интервала определяется значение признака, которое является модой:

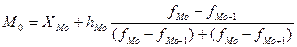, (5.1)

где 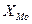-нижняя граница модального интервала;

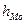- величина модального интервала;

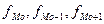- частота модального, предмодального и послемодального интервалов соответственно.

Медиана – варианта, которая делит ранжированный ряд на две равные части.

Медиана в дискретном ряду – варианта, расположенная в середине ряда. Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных вариант.

В интервальном вариационном ряду порядок нахождения медианы следующий: располагаем варианты по ранжиру, определяем накопленные (кумулятивные) частоты, находим медианный интервал. Он соответствует интервалу, кумулятивная частота которого равна или превышает половину суммы частот.

Медиана в интервальном вариационном ряду определяется по формуле:

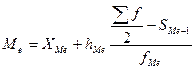, (5.2)

где 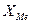– нижняя граница медианного интервала;

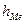- величина медианного интервала;

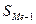- сумма накопленных частот, предшествующих медианному интервалу;

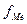- частота медианного интервала.