 Рис. 3.12.
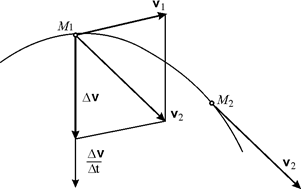
Рис. 3.12.
| Предположим, что в момент времени 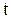 скорость точки равна скорость точки равна 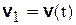 , а в момент времени , а в момент времени 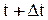 будет будет 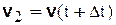 (рис. 3.12). Приращение вектора скорости (рис. 3.12). Приращение вектора скорости 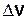 за промежуток времени за промежуток времени 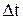 найдем как разность векторов найдем как разность векторов 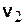 и и 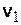 , ,
|
параллельно перенося вектор 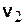 в точку М 1
в точку М 1
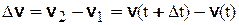 .
.
Отношение
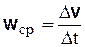
называется средним ускорением точки за промежуток времени 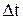 .
.
Ускорением 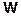 точки в данный момент времени называется предел отношения приращения скорости
точки в данный момент времени называется предел отношения приращения скорости 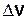 к приращению времени
к приращению времени 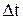 при условии, что последнее стремится к нулю, т.е.
при условии, что последнее стремится к нулю, т.е.
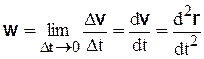 , (3.18)
, (3.18)
или 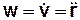 .
.
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса-вектора точки.
3.3.1. Ускорение при координатном способе задания движения
 2014-01-25
2014-01-25 704
704








