Равномерное движение. Равномерным называется такое движение точки, при котором модуль скорости все время остается постоянным; следовательно, и алгебраическая величина 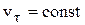 . Тогда
. Тогда
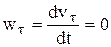 .
.
Если равномерное движение криволинейное, то ускорение точки будет представлено лишь нормальной составляющей 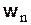 и
и 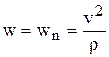 . В данном случае ускорение появляется только за счет изменения направления вектора скорости.
. В данном случае ускорение появляется только за счет изменения направления вектора скорости.
Если равномерное движение точки совершается по прямолинейной траектории, то 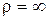 и
и 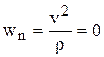 . В этом случае
. В этом случае 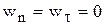 , а значит и
, а значит и 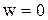 . Отметим, что равномерное прямолинейное движение является единственным движением, в котором ускорение точки все время равно нулю.
. Отметим, что равномерное прямолинейное движение является единственным движением, в котором ускорение точки все время равно нулю.
Найдем закон равномерного движения. Из формулы (3.16) имеем 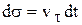 . Если в начальный момент времени
. Если в начальный момент времени 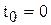 точка имеет координату
точка имеет координату 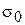 , то, беря от левой и правой частей равенства определенные интегралы (и учитывая, что
, то, беря от левой и правой частей равенства определенные интегралы (и учитывая, что 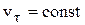 ), получим
), получим
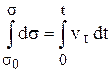 или
или 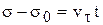 .
.
Окончательно находим закон равномерного движения точки в виде
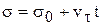 . (3.30)
. (3.30)
Равнопеременное движение. Равнопеременным называется движение точки, при котором модуль касательного ускорения остается все время постоянной: 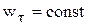 .
.
Найдем закон этого движения, считая, что при 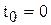
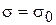 и
и 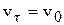 . Согласно первой из формул (3.27),
. Согласно первой из формул (3.27), 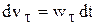 . Взяв от обеих частей этого равенства интегралы (учитывая, что
. Взяв от обеих частей этого равенства интегралы (учитывая, что 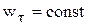 ), получим закон изменения скорости при равнопеременном движении
), получим закон изменения скорости при равнопеременном движении
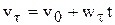 . (3.31)
. (3.31)
Формулу (3.31) представим в виде
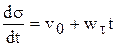 или
или 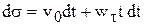 .
.
Интегрируя обе части этого равенства, найдем закон равнопеременного движения точки
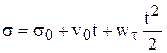 . (3.32)
. (3.32)
Величина скорости при равнопеременном движении меняется по закону (3.31). Если модуль скорости возрастает, то движение называется ускоренным, а если убывает – замедленным. При ускоренном движении величины 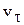 и
и 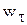 имеют одинаковые знаки (угол между
имеют одинаковые знаки (угол между 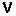 и
и 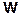 – острый), при замедленном движении величины
– острый), при замедленном движении величины 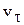 и
и 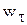 имеют разные знаки (угол между
имеют разные знаки (угол между 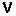 и
и 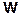 – тупой).
– тупой).
В случае равнопеременного прямолинейного движения точки 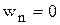 и в выражениях (3.31) и (3.32) следует принять
и в выражениях (3.31) и (3.32) следует принять 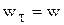 .
.
 2014-01-25
2014-01-25 805
805








