Вычисление проекций силы.
Сложение и разложение сил.
Аксиомы статики.
Основные задачи статики.
Вопросы
1. Основными задачами статики являются:
а) преобразование различных систем сил в более простые, им эквивалентные;
б) определение условий равновесия твердых тел, находящихся под действием различных систем сил.
Аксиома 1. Твердое тело под действием двух сил будет находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны (рис. 1.1).
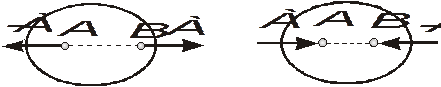
Рис. 1.1. Равновесие тела под действием двух сил
Аксиома 2. Действие любой системы сил на твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил.
Следствие: Силу, не изменяя ее действия на твердое тело, можно переносить вдоль линии ее действия (рис.1.2) Данное обстоятельство позволяет считать силы в теоретической механике скользящими векторами.
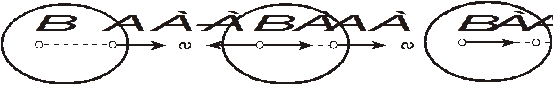
Рис. 1.2. Перенос силы вдоль ее линии действия
Аксиома 3. (Правило параллелограмма). Две силы, приложенные в одной точке, имеют равнодействующую, определяемую диагональю параллелограмма, построенного на этих силах и приложенную в этой же точке (рис. 1.3).
Говорят также, что в данном случае равнодействующая К равна геометрической или векторной сумме сил А! и А@. 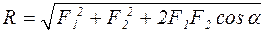 .
.
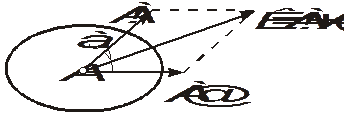
Рис. 1.3. Геометрическое сложение двух сил
Аксиома 4. Силы взаимодействия двух тел равны по величине и направлены вдоль одной прямой в противоположные стороны (третий закон Ньютона). Отметим, что в данном случае эти силы не уравновешивают друг друга так как приложены к разным телам (рис. 1.4).
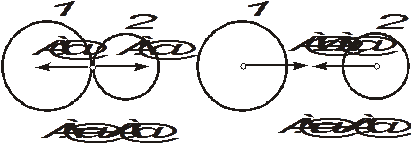
Рис. 1.4. Иллюстрация третьего закона Ньютона
Аксиома 5. (Принцип освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если заменить все связи эквивалент-ными им по воздействию на тело силами, называемыми реакциями связей.
Аксиома 6. Равновесие деформируемого тела не нарушится, если тело считать абсолютно твердым (другими словами: равновесие тела не нарушается при наложении на него дополнительных связей).
3. Сложение и разложение сил.
Различают геометрические и аналитический способы сложения сил. Рассмотрим первые из них.
Известно (аксиома 3), что два вектора можно сложить по правилу параллелограмма. Очевидно, что правилу параллелограмма эквивалентно правило треугольника (рис. 1.5). Последовательное применение правила треугольника позволяет определить геометрическую сумму нескольких сил (правило построения векторного многоугольника). Три вектора, не лежащие в одной плоскости, можно сложить используя правило параллелепипеда (рис.1.7).
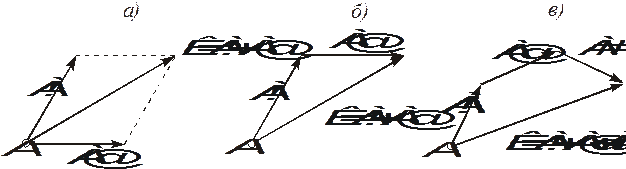
Рис. 1.5. Правила сложения векторов: а) параллелограмма, б) треугольника, в) построение векторного многоугольника
Для разложения силы на две составляющие (т.е. замене одной силы системой двух сил, эквивалентных исходной силе) используют правило параллелограмма (рис 1.6). Заметим, что решение данной задачи не является однозначным.
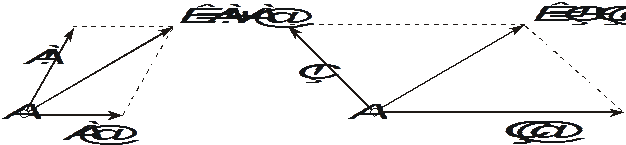
Рис. 1.6. Разложения векторов на составляющие
В пространстве силу можно разложить на три составляющие используя правило параллелепипеда (рис.1.7).
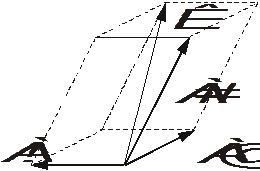
Рис. 1.7. Разложения вектора К на составляющие А!, А@, А# по правилу параллелепипеда
Обычно при решении конкретных задач силы раскладывают на составляющие, параллельные осям прямоугольной декартовой системы координат. Алгебраические значения таких составляющих называются проекциями силы на координатные оси.
Проекция считается положительной, если направление ее составляющей совпадает с положительным направлением соответствующей координатной оси. На рис. 1.8 приведены основные случаи, встречающиеся на практике при вычислении проекций векторов на оси прямоугольной системы координат.
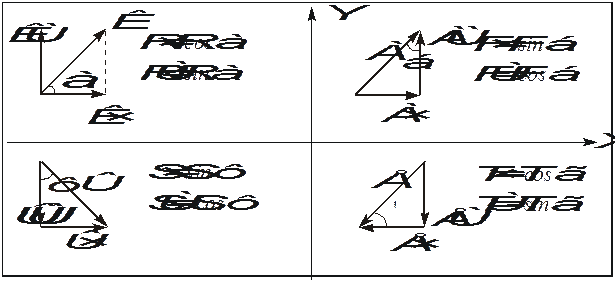
Рис. 1.8. Вычисление проекций силы на координатные оси
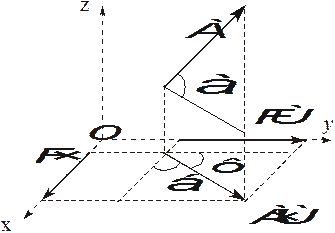
Иногда для вычисления проекций на оси приходится предварительно находить проекцию этой силы на плоскость (рис. 1.9)
|
Fxy=Fcosa,
Fx=Fxycosb= Fcosa cosb,
Fy=Fxy cosф=Fcosa cosф,
где А xy - проекция силы А на плоскость (величина векторная).
Рис. 1.9. К определению проекции силы на плоскость
 2014-01-25
2014-01-25 1003
1003








