Рассмотрим совокупность N невзаимодействующих квантовых частиц (фермионов или бозонов[30]) помещенных в объем V. Квантование энергии в трехмерном случае определяется формулой
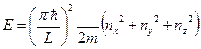 .
.
Из этой формулы можно получить число энергетических состояний в интервале dE.
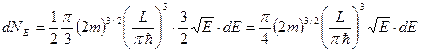 .
.
Отсюда получаем функцию плотности числа энергетических состояний
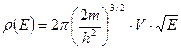 . (116)
. (116)
Теперь рассмотрим один энергетический уровень, представляя его открытой термодинамической системой (по температуре и числу частиц, большой канонический ансамбль). Большая статистическая сумма уровня
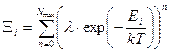 . (117)
. (117)
Для фермионов Nmax = 1, для бозонов Nmax = ¥. Проведя суммирование, получаем
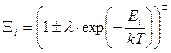 . (118)
. (118)
Плюс в формуле соответствует фермионам, минус бозонам.
Большая статистическая сумма всех уровней равна бесконечному произведению статистических сумм.
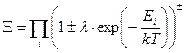 . (119)
. (119)
Термодинамика определяется логарифмом статистической суммы.
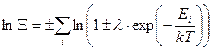 . (120)
. (120)
Суммирование можно заменить интегрированием, используя формулу плотности числа состояний
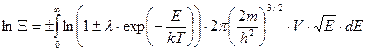 . (121)
. (121)
Используя формулу (37), получаем
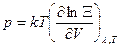
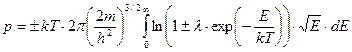
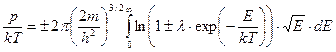 . (122)
. (122)
Чтобы окончательно получить термическое уравнение квантового газа нужно решить две проблемы. Определить l и вычислить интеграл (122). Величину l определим из условия фиксированного числа частиц. Используя (37), запишем
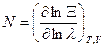
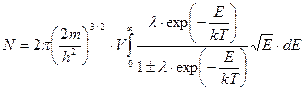 . (123)
. (123)
Запишем интегралы (122) и (123) через новую переменную 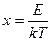 .
.
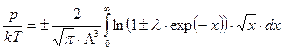 . (122¢)
. (122¢)
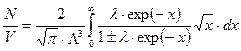 . (123¢)
. (123¢)
Здесь 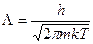 тепловая длина волны.
тепловая длина волны.
Теперь следует подынтегральные функции (122¢) и (123¢) разложить в ряды по переменной 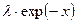 и проинтегрировать первые слагаемые.
и проинтегрировать первые слагаемые.
Ряд логарифма
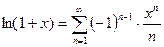
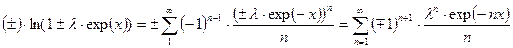 . [31]
. [31]
В формуле (122) возникают интегралы
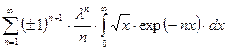 .
.
Вычислим один из интегралов
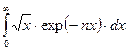 .
.
Перейдем к новой переменной 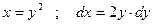 .
.
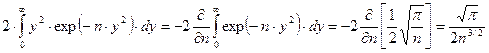 .
.
Теперь можно записать результат интегрирования (122¢)
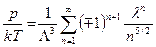 . (124)
. (124)
Ряд подынтегральной функции (123¢)
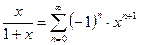 .
.
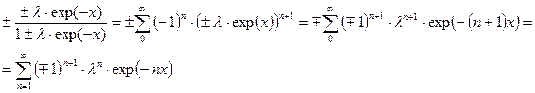 .
.
В формуле (123¢) возникают интегралы аналогичные предыдущим
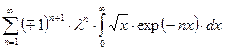 .
.
Можно записать результат интегрирования.
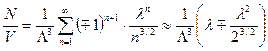 . (125)
. (125)
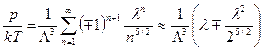 . (124)
. (124)
Уравнение (125) относительно l (малой величины) решаем методом последовательных приближений. Пренебрегая величиной второго порядка малости (l2) получаем первое приближение[32]
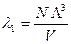 .
.
Подставляем l1 в «малое» слагаемое уравнения (125) и получаем l во втором приближении
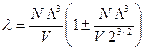 .
.
Теперь это значение l подставляем в уравнение (124), при этом в слагаемое второго порядка можно подставить l в первом приближении.
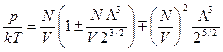 .
.
После преобразования
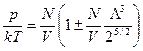 .
.
Окончательно термическое уравнение состояния квантового газа можно представить в виде
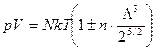 . (127)
. (127)
Плюс соответствует идеальному газу фермионов, минус идеальному газу бозонов. Квантовые поправки становятся существенными при высокой плотности частиц и низкой температуре. Или когда «квантовая тепловая ячейка» становится сравнимой с объемом, приходящимся на одну частицу 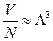 .
.
 2014-01-25
2014-01-25 784
784








