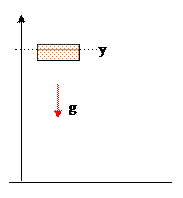
Рассмотрим небольшой объем идеального газа, находящийся в гравитационном поле. Статистический интеграл в этом случае запишется в виде[21]
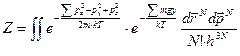 . (50)
. (50)
К «кинетической» экспоненте добавляется экспонента «потенциальная». Так как, координату y для всех частиц газа можно считать величиной постоянной, то результат интегрирования получить достаточно просто.
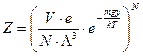 . (51)
. (51)
Химический потенциал определится формулой
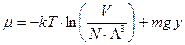 . (52)
. (52)
Преобразуем первое слагаемое к давлению.
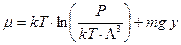 . (53)
. (53)
Теперь будем рассматривать большой объем газа (высокий сосуд). Известно, что химический потенциал является интенсивным параметром и постоянен по всему пространству сосуда (химический потенциал частиц газа одинаков на разных высотах). Приравниваем химические потенциалы газа на высоте y и y = 0.
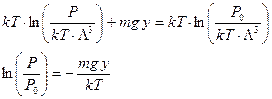
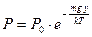 . (54)
. (54)
Получили формулу зависимости «давления атмосферы» от высоты (при постоянной температуре по высоте). Формулу удобнее записывать через молярные величины.
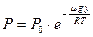 . (55)
. (55)
9. «Распределение Максвелла». [22](Функция плотности вероятности модуля скорости).
Рассмотрим одну частицу идеального газа. Ее можно считать термодинамической системой помещенной в термостат (выделенной частице предоставлен весь объем идеального газа). Запишем формулу дифференциальной вероятности состояния частицы в фазовом пространстве (канонический ансамбль).
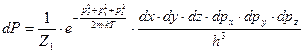 .
.
Так как 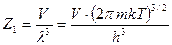 , то
, то
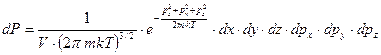 . (56)
. (56)
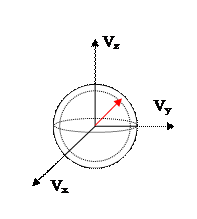
Перейдем в пространство скоростей (трехмерное пространство). Для этого нужно проинтегрировать выражение (56) по координатам и «расписать» импульсы.
 |
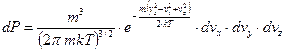 . (57)
. (57)Теперь перейдем в пространство модуля скорости (одномерное пространство). Для этого нужно проинтегрировать по объему шарового слоя пространства скоростей.
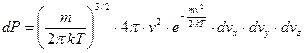 . (58)
. (58)
Отсюда получаем функцию плотности вероятности модуля скорости частиц идеального газа.
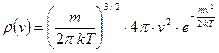 . (59)
. (59)
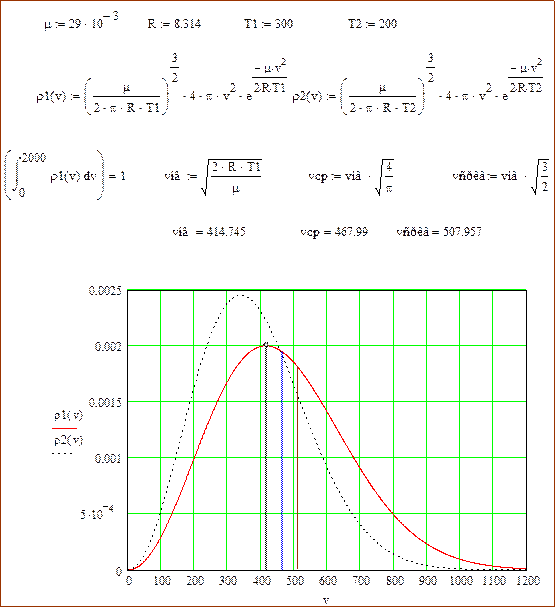
Приводим листинг среды MathCAD построения графика функции плотности и проверки ее нормировки для воздуха при температурах 200 °К и 300 °К.
Вычислим «характерные» скорости распределения. Скорость, соответствующая максимуму распределения
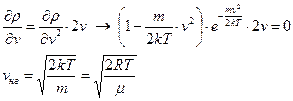 . (60)
. (60)
Среднее значение модуля скорости
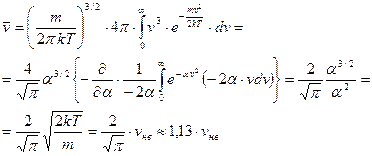 . (61)
. (61)
Среднеквадратичное значение скорости.
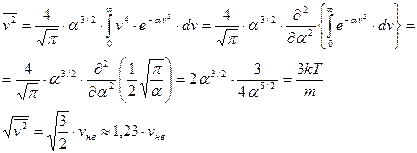 . (62)
. (62)
Примеры значений характерных скоростей показаны на вышеприведенном листинге MathCAD.
10. Закон равномерного распределения энергии по степеням свободы (Л.Д. Ландау).
Рассмотрим классическую систему с n степенями свободы. В большинстве случаях энергия такой системы может быть записана в квадратичном виде (в обобщенных координатах и скоростях)[23].
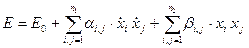 . (63)
. (63)
Общее число термодинамических степеней свободы равно сумме кинетических и потенциальных степеней свободы
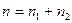 .
.
Статистический интеграл системы в термостате принимает вид (в константе С «спрятаны» и квантовая ячейка и факториал)
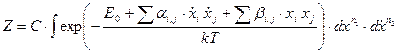 . (64)
. (64)
Сделаем преобразование координат (bi, j не путать с 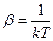 )
)
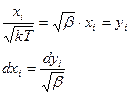 . (65)
. (65)
После преобразования
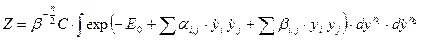 . (66)
. (66)
интеграл перестал зависеть от температуры. Пределы интегрирования можно считать остались прежними (бесконечными). Поэтому, зависимость статистического интеграла от температуры можно записать в виде
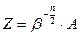 . (67)
. (67)
Где А – функция независящая от температуры. Используя полученную формулу (67) вычислим энергию системы.
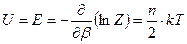 .
.
Мы видим, что энергия системы линейно зависит от числа степеней свободы и на одну степень свободы приходится энергия равная 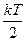 .
.
Для N – частичной системы без взаимодействия (идеальный газ) число степеней свободы можно представить так
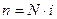 .
.
Где i – число степеней свободы одной частицы. Таким образом, энергия идеального газа
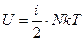 . (68)
. (68)
Для моля 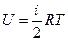 .
.
Определим «стандартные» мольные теплоемкости идеального газа (C v и C p). Запишем первый закон термодинамики для идеального газа с учетом формулы (68)
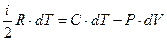 .
.
Отсюда (используем уравнение идеального газа для вычисления производной 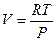 )
)
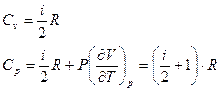 . (69)
. (69)
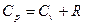 . (70)
. (70)
Таким образом, чисто классический идеальный газ должен обладать постоянной теплоемкостью.
 2014-01-25
2014-01-25 783
783








